练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

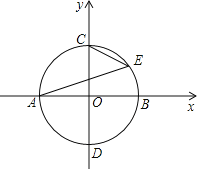
    【题目】如图，在直角坐标系中，以坐标原点为圆心、半径为1的⊙O与x轴交于A，B两点，与y轴交于C，D两点．E为⊙O上在第一象限的某一点，直线BF交⊙O于点F，且∠ABF=∠AEC，则直线BF对应的函数表达式为______．

    【答案】y＝－x＋1或y＝x－1

    【解析】

    试题由题意可知，∠AEC=∠AOC=45°；当∠ABF=∠AEC=45°时，只有点F与点C或D重合，根据待定系数法可求出直线BF对应的函数表达式．

    根据圆周角定理得，∠AEC=∠AOC=45°，

    ∵∠ABF=∠AEC=45°，

    ∴点F与点C或D重合；

    当点F与点C重合时，设直线BF解析式y=kx+b，

    ∴直线BF的解析式为y＝－x＋1，

    当点F与点D重合时，同理可得y＝x－1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校开展以感恩教育为主题的艺术活动，举办了四个项目的比赛，它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加，且限报一项活动。以九年级(1)班为样本进行统计，并将统计结果绘成如图1、图2所示的两幅统计图。请你结合图示所给出的信息解答下列问题。

    (1)求出参加绘画比赛的学生人数占全班总人数的百分比?

    (2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?

    (3)若该校九年级学生有600人，请你估计这次艺术活动中，参加演讲和唱歌的学生各有多少人?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，抛物线的顶点D的坐标为（1，-4），且与y轴交于点

    C（0，3）

    求该函数的关系式；

    求改抛物线与x轴的交点A，B的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学兴趣小组的同学在一次数学活动中，为了测量某建筑物AB的高，他们来到与建筑物AB在同一平地且相距12米的建筑物CD上的C处观察，测得某建筑物顶部A的仰角为30°、底部B的俯角为45°．求建筑物AB的高（精确到1米）．（可供选用的数据：≈1.4，≈1.7）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°，根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？（结果取整数）

    （参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81，≈1.41，≈1.73，≈2.24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠A＝36°，AB＝AC，∠ABC的平分线BE交AC于E．

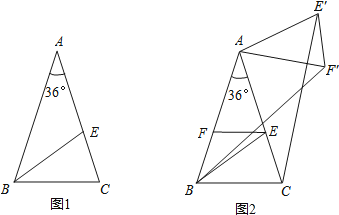
    （1）求证：AE＝BC；

    （2）如图2，过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′、BF′，求证：CE′＝BF′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创年利润情况进行统计，并绘制如图1，图2统计图．

    （1）求抽取员工总人数，并将图补充完整；

    （2）每人所创年利润的众数是 ，每人所创年利润的中位数是 ，平均数是 ；

    （3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游。

    [来

    根据以上信息，解答下列问题：

    （1）设租车时间为小时，租用甲公司的车所需费用为元，租用乙公司的车所需费用为元，分别求出，关于的函数表达式；

    （2）请你帮助小明计算并选择哪个出游方案合算。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数的顶点为点D．

    （1）求点D的坐标（用含m的代数式表示）；

    （2）求函数的图象与x轴的交点坐标；

    （3）若函数的图象在直线y=m的上方，求m的取值范围．

    查看答案和解析>>

    同步练习册答案