
【题目】(2016湖北襄阳第20题)
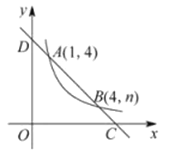
如图,直线y=ax+b与反比例函数y=![]() (x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(1)m= ,n= ;若M(xl,y1),N(x2,y2)是反比例函数图象上两点,且0<xl<x2,则yl y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
科目:初中数学 来源: 题型:
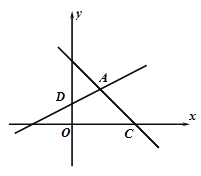
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]()
(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),当
重合),当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b,当x=2时y的值是﹣1,当x=﹣1时y的值是5.
(1)求此一次函数的解析式;
(2)若点P(m,n)是此函数图象上的一点,﹣3≤m≤2,求n的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小灵通家住黄河边的开封市,黄河大堤高出地面20米,另有开封铁塔高约58米,是开封市的一大景观.小灵通和好朋友明明、玲玲出去玩,小灵通站在黄河大堤上,玲玲站在地面放风筝,顽皮的明明则爬上了铁塔顶.小灵通说:“以大堤为基准,记为0米,则玲玲所在的位置高为-20米,明明所在的位置高为+58米”.明明说:“以铁塔顶为基准,记为0米,则玲玲所在的位置高为-58米,小灵通所在的位置高为-38米”.玲玲说:“明明的位置比我高58米”.他们谁说得对(如图)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学学生步行到郊外旅游.七(1)班学生组成前队,步行速度为4千米/时,七(2)班学生组成后队,速度为 6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com