
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]()
(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),当
重合),当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标
的坐标
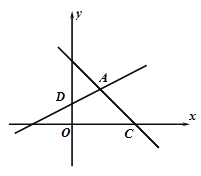
【答案】(1)![]() ;(2)(3,
;(2)(3,![]() ),(2,2).
),(2,2).
【解析】
试题分析:(1)首先设出一次函数解析式,将点A,D代入即可求出一次函数解析式;(2)先写出OB,OD,BC的长度,然后分两种情况讨论1:△BOD∽△BCE;2:△BOD∽△BEC.
试题解析:(1)设直线AD的解析式为y=kx+b
将点A![]() 代入直线y=kx+b中得:
代入直线y=kx+b中得: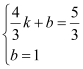
解得:![]()
![]() 直经AD的解析式为:
直经AD的解析式为:![]()
(2)设点E的坐标为(m,![]() m+1)
m+1)
令![]() 得x=-2
得x=-2
![]() 点B的坐标为(-2,0)
点B的坐标为(-2,0)
令y=-x+3=0得x=3
![]() 点C的坐标为(3,0)
点C的坐标为(3,0)
![]() OB=2, OD=1, BC=5, BD=
OB=2, OD=1, BC=5, BD=![]()
1. 当△BOD∽△BCE时,如图(1)所示,过点C作CE![]() BC交直线AB于E:
BC交直线AB于E:
![]()
![]()
![]()
![]() CE=
CE=![]()
![]()
![]() m+1=
m+1=![]() ,解得m=3
,解得m=3
![]() 此时E点的坐标为(3,
此时E点的坐标为(3,![]() )
)
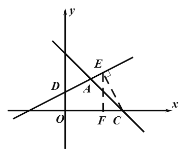
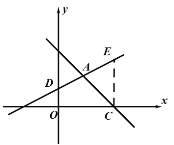
2. △BOD∽△BEC时,如图(2)所示,过点E作EF![]() BC于F点,则:
BC于F点,则:
![]()
![]()
![]()
![]() CE=
CE=![]()
![]() BE=
BE=![]()
![]()
![]() BE*CE=
BE*CE=![]() EF*BC
EF*BC
![]()
![]()
![]() EF=2
EF=2
![]()
![]() 解得m=2
解得m=2
![]() 此时E点的坐标为(2,2)
此时E点的坐标为(2,2)
![]() 当△BOD与△BCE相似时,满足条件的E坐标(3,
当△BOD与△BCE相似时,满足条件的E坐标(3,![]() ),(2,2).
),(2,2).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=2x+m(m>0)与x轴交于点A(﹣2,0),直线y=﹣x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若点P为x轴上一动点,且使PD+PC的值最小,不写过程,直接写出点P的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中正确的是( )
A. (-5)-(-3)=-8 B. (+5)-(-3)=2
C. (-5)-(+3)=-8 D. (-5)-(+3)=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了合理疏导交通,需要对我区6000名中学生上学出行方式进行统计,调取100名志愿者,随机调查了10所学校500名中学生的出行方式,本次调查中样本容量是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
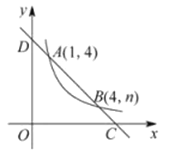
【题目】(2016湖北襄阳第20题)
如图,直线y=ax+b与反比例函数y=![]() (x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(1)m= ,n= ;若M(xl,y1),N(x2,y2)是反比例函数图象上两点,且0<xl<x2,则yl y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com