
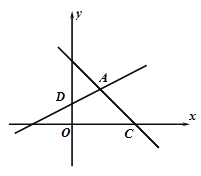
【题目】直线y=2x+m(m>0)与x轴交于点A(﹣2,0),直线y=﹣x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若点P为x轴上一动点,且使PD+PC的值最小,不写过程,直接写出点P的坐标。

【答案】(1)D点坐标为(﹣![]() ,
, ![]() );
);
(2)四边形AOCD的面积=![]() ;
;
(3)点E的坐标为(2![]() ﹣2,0)、(﹣2
﹣2,0)、(﹣2![]() ﹣2,0)、(2,0)、(0,0).
﹣2,0)、(2,0)、(0,0).
【解析】试题分析:(1)先把A点坐标代入y=2x+m得到m=4,则y=-2x+4,再利用AB=4可得到B点坐标为(2,0),则把B点坐标代入y=-x+n可得到n=2,则y=-x+2,然后根据两直线相交的问题,通过解方程组![]() 得到D点坐标;
得到D点坐标;
(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB-S△COB进行计算即可;(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=![]() ,然后分类讨论:当AE=AC=
,然后分类讨论:当AE=AC=![]() 时,以A点为圆心,2
时,以A点为圆心,2![]() 画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
试题解析:(1)把A(﹣2,0)代入y=2x+m得﹣4+m=0,
解得m=4,
∴y=﹣2x+4,
∵AB=4,A(﹣2,0),
∴B点坐标为(2,0),
把B(2,0)代入y=﹣x+n得﹣2+n=0,
解得n=2,
∴y=﹣x+2,
解方程组![]() 得
得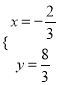 ,
,
∴D点坐标为(﹣![]() ,
, ![]() );
);
(2)当x=0时,y=﹣x+2=2,
∴C点坐标为(0,2),
∴四边形AOCD的面积=S△DAB﹣S△COB=![]() ×4×
×4×![]() ﹣
﹣![]() ×2×2=
×2×2=![]() ;
;
(3)∵A(﹣2,0),C(0,2),
∴AC=![]() ,
,
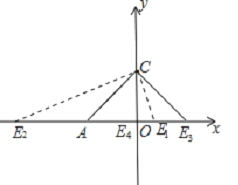
当AE=AC=![]() 时,E1点的坐标为(
时,E1点的坐标为(![]() ﹣2,0),E2点的坐标为(﹣
﹣2,0),E2点的坐标为(﹣![]() ﹣2,0);
﹣2,0);
当CE=CA时,E3点的坐标为(2,0),
当EA=EC时,E4点的坐标为(0,0),
综上所述,点E的坐标为(![]() ﹣2,0)、(﹣
﹣2,0)、(﹣![]() ﹣2,0)、(2,0)、(0,0).
﹣2,0)、(2,0)、(0,0).


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
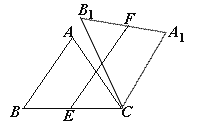
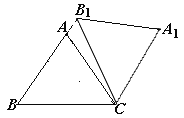
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生在2015年11月第2周星期五股市收盘时,以每股9元的价格买进某公司的股票1000股,在11月第3周的星期一至星期五,该股票每天收盘时每股的涨跌(单位:元)情况如下表:

注:表中记录的数据为每天收盘价格与前一天收盘价格的变化量,星期一的数据是与上星期五收盘价格的变化量.
(1)请你判断在11月的第3周内,该股票价格收盘时,价格最高的是哪一天?
(2)在11月第3周内,求李先生购买的股票每股每天平均的收盘价格.(结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]()
(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),当
重合),当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)直接写出m= ,n= ;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围 ;
成立的x的取值范围 ;
(3)在x轴上找一点P使PA+PB的值最小,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小灵通家住黄河边的开封市,黄河大堤高出地面20米,另有开封铁塔高约58米,是开封市的一大景观.小灵通和好朋友明明、玲玲出去玩,小灵通站在黄河大堤上,玲玲站在地面放风筝,顽皮的明明则爬上了铁塔顶.小灵通说:“以大堤为基准,记为0米,则玲玲所在的位置高为-20米,明明所在的位置高为+58米”.明明说:“以铁塔顶为基准,记为0米,则玲玲所在的位置高为-58米,小灵通所在的位置高为-38米”.玲玲说:“明明的位置比我高58米”.他们谁说得对(如图)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com