
【题目】如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.
【答案】解:∵∠ABE+∠EBC=∠ABC=90°,
∠E'BC+∠EBC=∠E'BE=90°,
∴∠ABE=∠E'BC,
在△ABE与△CBE'中, ,
,
∴△ABE≌△CBE'(SAS),
∴CE'=AE=1,
∵∠EBE'=90°,BE=BE'=2,
∴EE'2=22+22=8,
∵∠EBE'=90°,BE=BE',
∴∠BE'E=45°,
∵∠BE'C=135°,
∴∠EE'C=135°﹣45°=90°,
∴ ![]()
【解析】(1)根据∠ABC=90°,∠EBE′=90°,先证明∠ABE=∠E'BC,再利用全等三角形的判定证明△ABE≌△CBE',得出CE'=AE,然后证明∠EE'C=90°,利用勾股定理求出EE',在Rt△EE'C中,根据勾股定理求出EC的长即可。


科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.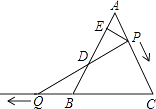
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.明天太阳从西方升起
B.打开电视机,正在播放广告
C.掷一枚硬币,正面朝上
D.任意一个三角形,它的内角和等于180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. a3a=a3 B. (2a+b)2=4a2+b2 C. a8b÷a2=a4b D. (﹣3ab3)2=9a2b6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】23 , 33 , 和43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和.83也能按此规律进行“分裂”,则83“分裂”出的奇数中最大的是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com