
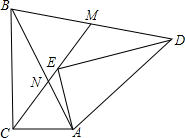
 如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.
如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.分析 (1)根据旋转的性质,△ABD和△ACE是等腰三角形,设∠BAE=x,根据等腰三角形的性质即可求得∠ACE=∠AEC=∠ABD=∠ADB=90°-$\frac{1}{2}$(α+x),进一步求得∠BMN=∠BAC=α,即可证得△BNM∽△CNA,得出$\frac{BN}{CN}$=$\frac{MN}{AN}$,进而证得△BCN∽△MNA,得出∠ABC=∠AMN,证得AM⊥BD,根据等腰三角形三线合一的性质即可证得结论;
(2)证得△CNA是等腰三角形,从而得出AN=2m•cosα,AB=$\frac{m}{cosα}$,进一步得出BN=AB-AN=$\frac{m}{cosα}$-2m•cosα,然后证得∠BNM=∠BMN,根据等角对等边证得BM=BN=$\frac{m}{cosα}$-2m•cosα,即可得出BD的长.
解答 (1)证明:将△ABC旋转一个角度后得到△AED,
则AB=AD,AC=AE,
∴△ABD和△ACE是等腰三角形,
∵∠BAC=α,设∠BAE=x,
∴∠CAE=α+x,
∵∠CAE=∠BAD=α+x,
∴∠ACE=∠AEC=∠ABD=∠ADB=$\frac{180-(α+x)}{2}$=90°-$\frac{1}{2}$(α+x),
∵∠BCM=90°-∠ACE=90°-[90°-$\frac{1}{2}$(α+x)]=$\frac{1}{2}$(α+x),
∠CBM=∠CBA+∠ABD=90°-α+90°-$\frac{1}{2}$(α+x)
在△BCM中,∠BMC=180°-∠CBM-∠BCM=190°-[90°-α+90°-$\frac{1}{2}$(α+x)]-$\frac{1}{2}$(α+x)=α,
∴∠BMN=∠BAC=α,
∵∠BNM=∠ANC,
∴△BNM∽△CNA,
∴$\frac{BN}{CN}$=$\frac{MN}{AN}$,
连接AM, ∵∠BNC=∠MNA,
∵∠BNC=∠MNA,
∴△BCN∽△MNA,
∴∠ABC=∠AMN,
∵∠ABC+∠BAC=90°,
∴∠BMN+∠AMN=90°,
∴AM⊥BD,
∴M为BD的中点;
(2)解:若CN=CA=m,则△CNA是等腰三角形,
∴∠CAB=∠ANC=α,
∴∠ACE=180°-2α,
∵∠ACE=90°-$\frac{1}{2}$(α+x),
∴180°-2α=90°-$\frac{1}{2}$(α+x),
∴x=3α-180°,
∵AN=2m•cosα,AB=$\frac{m}{cosα}$,
∴BN=AB-AN=$\frac{m}{cosα}$-2m•cosα,
∵∠BNM=∠ANC=α,∠CMB=α,
∴∠BNM=∠BMN,
∴BM=BN=$\frac{m}{cosα}$-2m•cosα,
∴BD=2BM=2m($\frac{1}{cosα}$-2cosα).
点评 本题考查了旋转的性质,相似三角形的判定和性质,等腰三角形的判定和性质,解直角三角形等,求得三角形相似是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 锻炼情况 | 女生 | 男生 |
| 天天锻炼 | 20 | 27 |
| 不经常锻炼 | 18 | 24 |
| 不锻炼 | 12 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
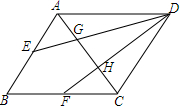 如图,在△ABC中,E,F分别为AB,BC边上的中点,G,H是AC的三等分点,EG,FH的延长线交于点D.求证:①DG:EG=2:1;②四边形ABCD是平行四边形.
如图,在△ABC中,E,F分别为AB,BC边上的中点,G,H是AC的三等分点,EG,FH的延长线交于点D.求证:①DG:EG=2:1;②四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
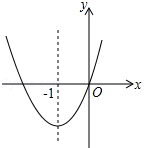 如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )
如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com