
【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.

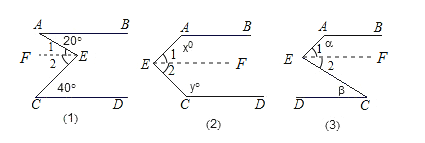
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
【答案】(1)60;(2) 360°﹣x°﹣y°(3)详见解析
【解析】首先都需要过点E作EF∥AB,由AB∥CD,可得AB∥CD∥EF.
(1)根据两直线平行,内错角相等,即可求得∠AEC的度数;
(2)根据两直线平行,同旁内角互补,即可求得∠AEC的度数;
(3)根据两直线平行,内错角相等;两直线平行,同旁内角互补,即可求得∠AEC的度数.
如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
(1)∵∠A=20°,∠C=40°,
∴∠1=∠A=20°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=60°;
(2)∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=x°,∠C=y°,
∴∠1+∠2+x°+y°=360°,
∴∠AEC=360°﹣x°﹣y°;
(3)∠A=α,∠C=β,
∴∠1+∠A=180°,∠2=∠C=β,
∴∠1=180°﹣∠A=180°﹣α,
∴∠AEC=∠1+∠2=180°﹣α+β.
![]()


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同位角相等
B.同一平面内的两条不重合的直线有相交、平行和垂直三种位置关系
C.三角形的三条高线一定交于三角形内部同一点
D.三角形三条角平分线的交点到三角形三边的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC= ![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 . 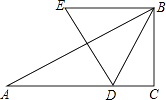
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y= ![]() (k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S. 
(1)求k的值;
(2)当S= ![]() 时,求P点的坐标;
时,求P点的坐标;
(3)写出S关于m的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() 、
、![]() 、
、![]() ;
;
求作:△ABC,使![]() ,
, ![]() ,
, ![]() ;
;

【答案】答案见解析
【解析】试题分析:先画出与![]() 相等的角,再画出
相等的角,再画出![]() 的长,连接
的长,连接![]() ,则
,则![]() 即为所求三角形.
即为所求三角形.
试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15
【题目】已知:线段![]() ,
, ![]() ,求作:
,求作: ![]() ,使
,使![]() ,
, ![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com