
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
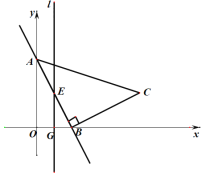
(1)求点![]() 的坐标;
的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
【答案】(1) C(6,2);(2) M(1,7);(3)见解析.
【解析】
(1)过点C作x轴的垂线,交x轴于点H,通过“角边角”易证![]() ≌
≌![]() ,得到BH=AO=4,CH=OB=2,即可得到C点坐标;
,得到BH=AO=4,CH=OB=2,即可得到C点坐标;
(2)根据题意可设点M(1,a),根据![]() 可得关于m的方程,然后求解方程即可;
可得关于m的方程,然后求解方程即可;
(3)由(2)可得CE=5,EM=5,CM=![]() ,根据勾股定理的逆定理即可得到
,根据勾股定理的逆定理即可得到![]() 是等腰直角三角形.
是等腰直角三角形.
解:(1)过点C作x轴的垂线,交x轴于点H,

∵![]() ,
,
∴A(0,4),B(2,0),
∵BA=BC,
∴![]() ≌
≌![]() (ASA),
(ASA),
∴BH=AO=4,CH=OB=2,
∴C(6,2)
(2)如图,由题意可知点G(1,0),点E(1,2),
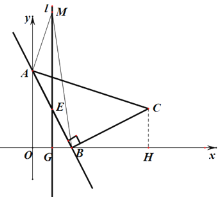
∵AB=BC=2![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
设M(1,a),则![]() ,
,
解的a=7,
则M(1,7) ;
(3)联结CM,CE,
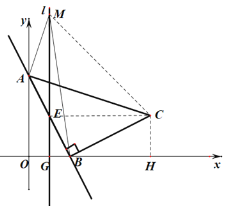
由于点E(1,2),C(6,2),M(1,7),
则CE=5,EM=5,CM=![]() ,
,
可得:![]() ,
,
CE=EM,
∴![]() 是等腰直角三角形.
是等腰直角三角形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3,∠BCD=80°,求∠ADC的度数.

解:∵∠1+∠2=180°,(已知)
∴ ∥ .( )
∴∠B=∠DEC.( )
∵∠B=∠3,(已知)
∴
∴AD∥BC,( )
∴ (两直线平行,同旁内角互补)
∵∠BCD=80°,
∴∠ADC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
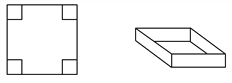
【题目】用一块边长为60cm的正方形薄钢片制作一个长方体盒子.
(1)如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,然后把四边折合起来(如图所示).设小正方形的边长为xcm,当做成盒子的底面积为900cm2时,求该盒子的高;
(2)如果要做成一个有盖的长方体盒子,其制作方案要求同时符合下列两个条件:
①必须在薄钢片四个角上各截去一个四边形(其余部分不能裁截);
②折合后薄钢片既无空隙又不重叠地围成各盒面.
请你画出符合上述制作方案的一种草图,并求当底面积为800cm2时,该盒子的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康.你知道吗,被动吸烟也大大危害着人类的健康.为此,联合国规定每年的5月31日为世界无烟日.为配合今年的“世界无烟日”宣传活动,小明和同学们在学校所在地区展开了以“我支持的戒烟方式”为主题的问卷调查活动,征求市民的意见,并将调查结果分析整理后,制成下列统计图:

(1)求小明和同学们一共随机调查了多少人?
(2)根据以上信息,请你把统计图补充完整;
(3)如果该地区有2万人,那么请你根据以上调查结果,估计该地区大约有多少人支持“强制戒烟”这种戒烟方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
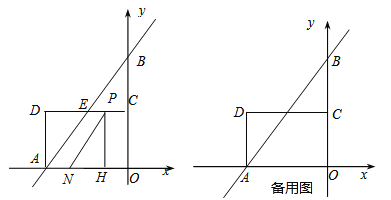
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m .设饲养室为长为x(m),占地面积为![]() .
.
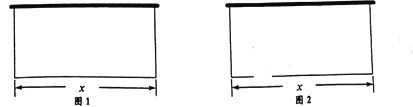
(1)如图![]() ,问饲养室为长x为多少时,占地面积y 最大?
,问饲养室为长x为多少时,占地面积y 最大?
(2)如图![]() ,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
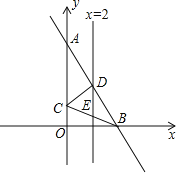
【题目】如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
(1)求证:∠OCB=2∠CBA;
(2)求点C的坐标和直线BC的解析式;
(3)求△DEB的面积;
(4)在x轴上存在一点P使PD-PC最长,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
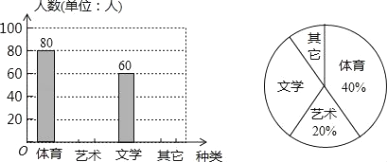
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com