
【题目】如图,∠1+∠2=180°,∠B=∠3,∠BCD=80°,求∠ADC的度数.

解:∵∠1+∠2=180°,(已知)
∴ ∥ .( )
∴∠B=∠DEC.( )
∵∠B=∠3,(已知)
∴
∴AD∥BC,( )
∴ (两直线平行,同旁内角互补)
∵∠BCD=80°,
∴∠ADC= .
【答案】AB∥DE;同旁内角互补,两直线平行;两直线平行,内错角相等;∠3=∠DEC;同位角相等,两直线平行;100°.
【解析】
根据平行线的判定得出AB∥DE,根据平行线的性质得出∠B=∠DEC,求出∠3=∠DEC,根据平行线的判定得出AD∥BC;根据平行线的性质得出∠ADC+∠BCD=180°,即可求出答案.
解:∵∠1+∠2=180°,(已知)
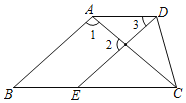
∴AB∥DE.(同旁内角互补,两直线平行)
∴∠B=∠DEC.(两直线平行,同位角相等)
∵∠B=∠3,(已知)
∴∠3=∠DEC
∴AD∥BC,(内错角相等,两直线平行)
∴∠ADC+∠BCD=180°,(两直线平行,同旁内角互补)
∵∠BCD=80°,∴∠ADC=100°.
故答案为:AB∥DE;同旁内角互补,两直线平行;两直线平行,内错角相等;∠3=∠DEC;同位角相等,两直线平行;100°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转90°后得到
顺时针旋转90°后得到![]() (点
(点![]() 的对应点是点
的对应点是点![]() ,点
,点![]() 的对应点是点
的对应点是点![]() ),连接
),连接![]() .若
.若![]() ,则
,则![]() 的大小是( )
的大小是( )
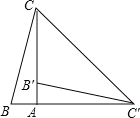
A. 77°B. 69°C. 67°D. 32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场设立了一个可以自由旋转的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组落在奖品“铅笔”区域的统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的成功率 |
(1).计算并完成表格(精确到0.01);
(2).请估计,当![]() 很大时,落在“铅笔”区域的频率将会接近______(精确到0.1).
很大时,落在“铅笔”区域的频率将会接近______(精确到0.1).
(3).假如你去转动该转盘一次,你获得铅笔的成功率约是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
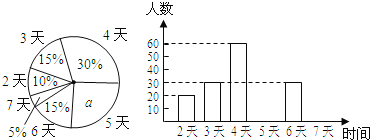
【题目】江都区教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)扇形统计图中a=____ ___,参加调查的八年级学生人数为___ __人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为____ ___;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校墙边有两根木杆.
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
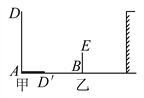
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
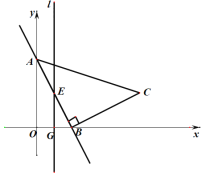
(1)求点![]() 的坐标;
的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com