
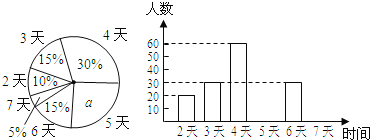
【题目】江都区教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)扇形统计图中a=____ ___,参加调查的八年级学生人数为___ __人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为____ ___;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人.
【答案】(1)25﹪,200 (2) 108°(3) 4500
【解析】
(1)扇形统计图中,根据单位1减去其他的百分比即可求出a的值;由参加实践活动为2天的人数除以所占的百分比即可求出八年级学生总数;
(2)求出活动时间为5天和7天的总人数,即可补全图形;用“活动时间为4天”的百分比乘以360°即可得出结果;
(3)求出活动时间不少于4天的百分比之和,乘以6000即可得到结果.
(1)根据题意得:a=1-(5%+10%+15%+15%+30%)=25%,
八年级学生总数为20÷10%=200(人);
(2)活动时间为5天的人数为200×25%=50(人),活动时间为7天的人数为200×5%=10(人),
补全统计图,如图所示:
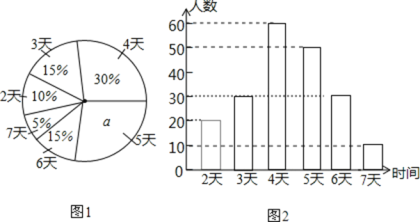
“活动时间为4天”的扇形所对应的圆心角的度数为:360°×30%=108°
(3)根据题意得:6000×(30%+25%+15%+5%)=4500(人),
则活动时间不少于4天的约有4500人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3,∠BCD=80°,求∠ADC的度数.

解:∵∠1+∠2=180°,(已知)
∴ ∥ .( )
∴∠B=∠DEC.( )
∵∠B=∠3,(已知)
∴
∴AD∥BC,( )
∴ (两直线平行,同旁内角互补)
∵∠BCD=80°,
∴∠ADC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行统计,并绘制出了如图1和图2所示的统计图,根据图中信息解答下列问题:

(1)这天共销售了多少个粽子?
(2)销售B品牌粽子多少个?并补全图1中的条形图;
(3)求出A品牌粽子在图2中所对应的圆心角的度数;
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
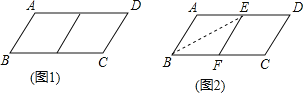
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行了如下操作:如图,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(2)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
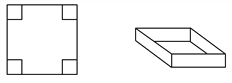
【题目】用一块边长为60cm的正方形薄钢片制作一个长方体盒子.
(1)如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,然后把四边折合起来(如图所示).设小正方形的边长为xcm,当做成盒子的底面积为900cm2时,求该盒子的高;
(2)如果要做成一个有盖的长方体盒子,其制作方案要求同时符合下列两个条件:
①必须在薄钢片四个角上各截去一个四边形(其余部分不能裁截);
②折合后薄钢片既无空隙又不重叠地围成各盒面.
请你画出符合上述制作方案的一种草图,并求当底面积为800cm2时,该盒子的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com