
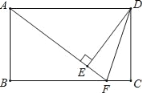
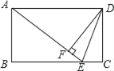
【题目】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证:
(1)△ABF≌△DEA;
(2)DF是∠EDC的平分线.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据矩形性质得出∠B=90°,AD=BC,AD∥BC,推出∠DAE=∠AFB,求出AF=AD,根据AAS证出即可;
(2)有全等推出DE=AB=DC,根据HL证△DEF≌△DCF,根据全等三角形的性质推出即可.
(1)∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠DEA=∠B=90°,
∵AF=BC,
∴AF=AD,
在△DEA和△ABF中
∵
∴△DEA≌△ABF(AAS);
(2)证明:∵由(1)知△ABF≌△DEA,
∴DE=AB,
∵四边形ABCD是矩形,
∴∠C=90°,DC=AB,
∴DC=DE.
∵∠C=∠DEF=90°
∴在Rt△DEF和Rt△DCF中
![]()
∴Rt△DEF≌Rt△DCF(HL)
∴∠EDF=∠CDF,
∴DF是∠EDC的平分线.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
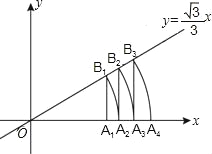
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
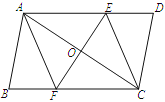
(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
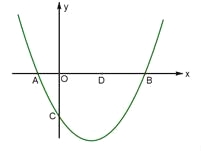
(1)b=______,点B的横坐标为_______(上述结果均用含c的代数式表示);
(2)连结BC,过点A作直线AE//BC,与抛物线交于点E.点D是x轴上一点,坐标为(2,0),当C、D、E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结PB、PC.设△PBC的面积为S.①求S的取值范围;②若△PBC的面积S为正整数,则这样的△PBC共有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.
求证:(1)DF=AB;
(2)DE是∠FDC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题
(1)本次调查共抽取了学生多少人?
(2)求本次调查中喜欢踢足球人数,并补全条形统计图;
(3)若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com