
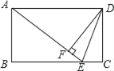
【题目】如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.
求证:(1)DF=AB;
(2)DE是∠FDC的平分线.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由矩形的性质得出AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,得出∠DAF=∠AEB,证出AD=AE,由AAS证明△ADF≌△EAB,即可得出结论;
(2)由HL证明Rt△DEF≌Rt△DEC,得出对应角相等∠EDF=∠EDC,即可得出结论.
(1)∵四边形ABCD是矩形,
∴AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,
∴∠DAF=∠AEB,
∵AE=BC,
∴AD=AE,
∵DF⊥AE,
∴∠AFD=∠DFE=90°,
∴∠AFD=∠B,
在△ADF和△EAB中, 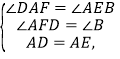
∴△ADF≌△EAB(AAS),
∴DF=AB;
(2)∵DF=AB,AB=DC,
∴DF=DC,
在Rt△DEF和Rt△DEC中, ![]()
∴Rt△DEF≌Rt△DEC(HL),
∴∠EDF=∠EDC,
∴DE是∠FDC的平分线.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积![]() __________,△ADE的面积
__________,△ADE的面积![]() ______________.
______________.
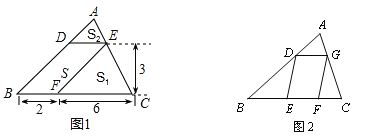
探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
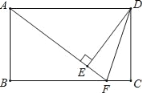
【题目】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证:
(1)△ABF≌△DEA;
(2)DF是∠EDC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
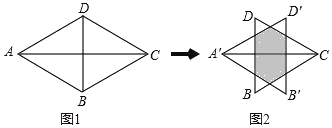
【题目】如图1,等边△ABD与等边△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=![]() 时,图中阴影部分为正六边形;③当k=
时,图中阴影部分为正六边形;③当k=![]() 时,图中阴影部分的面积是
时,图中阴影部分的面积是![]() ;正确的是( )
;正确的是( )
A. ①B. ①②C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
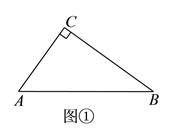
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
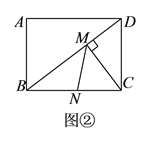
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
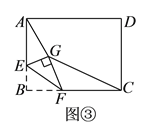
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
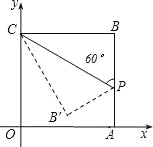
【题目】如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A. (2,2![]() )B. (
)B. (![]() ,
,![]() )C. (2,
)C. (2,![]() )D. (
)D. (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com