
【题目】如图1,等边△ABD与等边△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=![]() 时,图中阴影部分为正六边形;③当k=
时,图中阴影部分为正六边形;③当k=![]() 时,图中阴影部分的面积是
时,图中阴影部分的面积是![]() ;正确的是( )
;正确的是( )
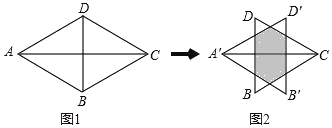
A. ①B. ①②C. ①③D. ①②③
【答案】C
【解析】
根据等边三角形的性质以及平移的性质,即可得到OM+MN+NR+GR+EG+OE=A′D′+CD=2+2=4;根据A′F![]() ,即可得到MO≠MN,进而得出阴影部分不是正六边形;阴影部分的面积=△A′B′D′的面积﹣△A′MN的面积﹣△OD′E的面积﹣△RGB′的面积,据此进行计算即可.
,即可得到MO≠MN,进而得出阴影部分不是正六边形;阴影部分的面积=△A′B′D′的面积﹣△A′MN的面积﹣△OD′E的面积﹣△RGB′的面积,据此进行计算即可.
解:∵两个等边△ABD,△CBD的边长均为2,将△ABD沿AC方向向右平移到△A′B′D′的位置,
∴A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′,
∴OM+MN+NR+GR+EG+OE=A′D′+CD=2+2=4,
故①正确;
∵k![]()
∴A′F![]()
∴A′M=A′F÷cos30°=1,MN=1.
∴![]()
∴MO≠MN,
∴阴影部分不是正六边形,
故②错误;
阴影部分的面积=△A′B′D′的面积﹣△A′MN的面积﹣△OD′E的面积﹣△RGB′的面积
![]()
![]()
故③正确,
故选:C.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
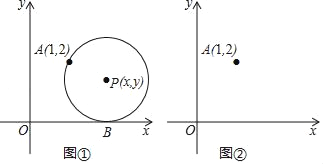
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
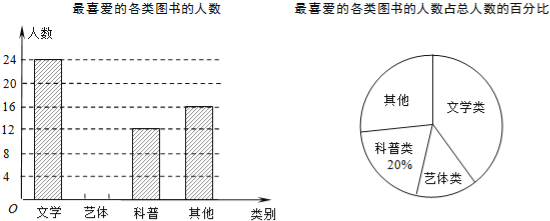
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整).
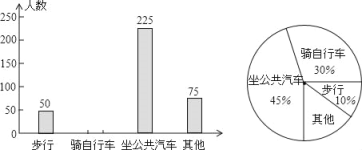
(1)此次共调查了多少位学生?
(2)将表格填充完整;
步行 | 骑自行车 | 坐公共汽车 | 其他 |
50 |
(3)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
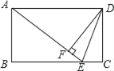
【题目】如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.
求证:(1)DF=AB;
(2)DE是∠FDC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
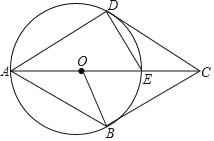
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ),射线
),射线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
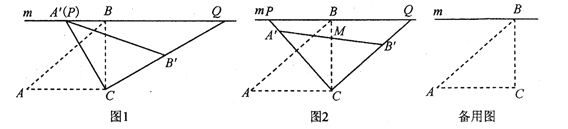
(1)如图1,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图2,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程中,当点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恩阳区市民广场有一棵高大的老黄角树树.小明为测量该树的高度AD,在大树前的平地上点C处测得大树顶端A的仰角∠C=31°,然后向前直走22米到达B处,又测得大树顶端A的仰角∠ABD=45°,已知C、B、D在同一直线上(如图所示),求老树的高度AD.(参考数据:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)


查看答案和解析>>
科目:初中数学 来源: 题型:
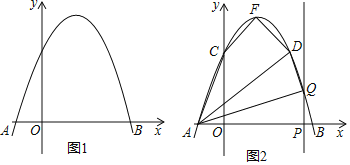
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com