
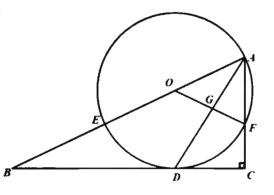
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
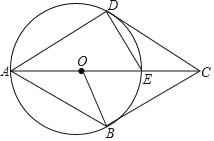
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)先判断出∠2+∠3=90°,再判断出∠1=∠2即可得出结论;
(2)根据等腰三角形的性质得到∠3=∠COD=∠DEO=60°,根据平行线的性质得到∠4=∠1,根据全等三角形的性质得到∠CBO=∠CDO=90°,于是得到结论;
(3)先判断出△ABO≌△CDE得出AB=CD,即可判断出四边形ABCD是平行四边形,最后判断出CD=AD即可.
(1)如图,连接OD,
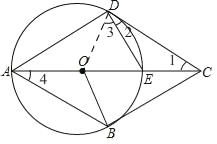
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠2+∠3=∠1+∠COD=90°,
∵DE=EC,
∴∠1=∠2,
∴∠3=∠COD,
∴DE=OE;
(2)∵OD=OE,
∴OD=DE=OE,
∴∠3=∠COD=∠DEO=60°,
∴∠2=∠1=30°,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴∠BOC=∠DOC=60°,
在△CDO与△CBO中,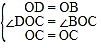 ,
,
∴△CDO≌△CBO(SAS),
∴∠CBO=∠CDO=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(3)∵OA=OB=OE,OE=DE=EC,
∴OA=OB=DE=EC,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴△ABO≌△CDE(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,
∴∠DAE=![]() ∠DOE=30°,
∠DOE=30°,
∴∠1=∠DAE,
∴CD=AD,
∴ABCD是菱形.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
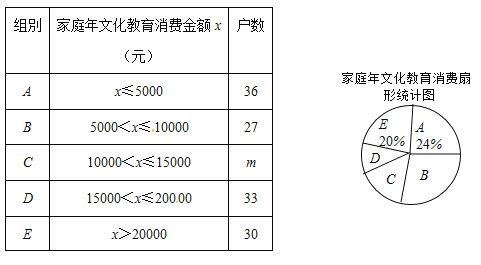
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
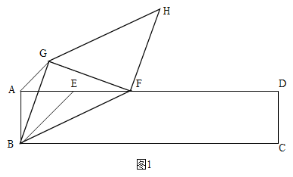
【题目】如图,矩形ABCD,AB=2,BC=10,点E为AD上一点,且AE=AB,点F从点E出发,向终点D运动,速度为1cm/s,以BF为斜边在BF上方作等腰直角△BFG,以BG,BF为邻边作BFHG,连接AG.设点F的运动时间为t秒.
(1)试说明:△ABG∽△EBF;
(2)当点H落在直线CD上时,求t 的值;
(3)点F从E运动到D的过程中,直接写出HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(![]() ,
,![]() ).如图,在平面直角坐标系xOy中,双曲线y=
).如图,在平面直角坐标系xOy中,双曲线y=![]() (x<0)和y=
(x<0)和y=![]() (x>0)的图象关于y轴对称,直线y=
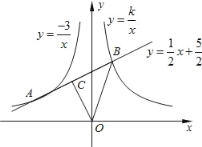
(x>0)的图象关于y轴对称,直线y=![]() 与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABD与等边△CBD的边长均为2,将△ABD沿AC方向向右平移k个单位到△A′B′D′的位置,得到图2,则下列说法:①阴影部分的周长为4;②当k=![]() 时,图中阴影部分为正六边形;③当k=
时,图中阴影部分为正六边形;③当k=![]() 时,图中阴影部分的面积是
时,图中阴影部分的面积是![]() ;正确的是( )
;正确的是( )
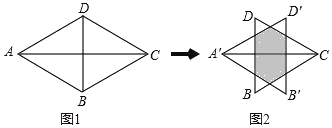
A. ①B. ①②C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
(1)m的取值范围是 ,函数图象的另一支位于第一象限,若x1>x2,y1>y2,则点B在第 象限;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点C与点A关于x轴对称,若△OAC的面积为6,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com