
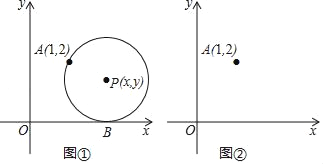
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
【答案】(1)![]() ;(2)图象为开口向上的抛物线,见解析;(3)点A;x轴;(4)
;(2)图象为开口向上的抛物线,见解析;(3)点A;x轴;(4)![]()
【解析】(1)由题意得到AP=PB,求出y的值,即为圆P的半径;
(2)利用两点间的距离公式,根据AP=PB,确定出y关于x的函数解析式,画出函数图象即可;
(3)类比圆的定义描述此函数定义即可;
(4)画出相应图形,求出m的值,进而确定出所求角的余弦值即可.
(1)由x=2,得到P(2,y),
连接AP,PB,
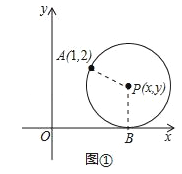
∵圆P与x轴相切,
∴PB⊥x轴,即PB=y,
由AP=PB,得到![]() =y,
=y,
解得:y=![]() ,
,
则圆P的半径为![]() ;
;
(2)同(1),由AP=PB,得到(x﹣1)2+(y﹣2)2=y2,
整理得:y=![]() (x﹣1)2+1,即图象为开口向上的抛物线,
(x﹣1)2+1,即图象为开口向上的抛物线,
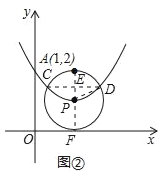
画出函数图象,如图②所示;
(3)给(2)中所得函数图象进行定义:此函数图象可以看成是到点A的距离等于到x轴的距离的所有点的集合;
故答案为:点A;x轴;
(4)连接CD,连接AP并延长,交x轴于点F,交CD于E,
设PE=a,则有EF=a+1,ED=![]() ,
,
∴D坐标为(1+![]() ,a+1),
,a+1),
代入抛物线解析式得:a+1=![]() (1﹣a2)+1,
(1﹣a2)+1,
解得:a=﹣2+![]() 或a=﹣2﹣
或a=﹣2﹣![]() (舍去),即PE=﹣2+
(舍去),即PE=﹣2+![]() ,
,
在Rt△PED中,PE=![]() ﹣2,PD=1,
﹣2,PD=1,
则cos∠APD=![]() =
=![]() ﹣2.
﹣2.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AB=BC,D在边 AC上,AE⊥BD于 E
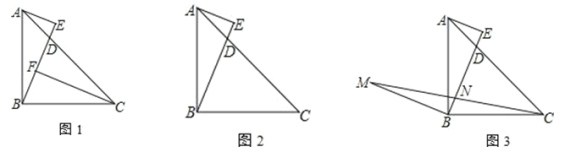
(1)如图1,作 CF⊥BD于F,求证:CF-AE=EF
(2)如图2,若 BC=CD,求![]() 的值
的值
(3)如图3,作 BM⊥BE,且 BM=BE,AE=2,EN=4,连 CM交 BE于 N,请直接写出△BCM的面积为___
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐对几何中角平分线的兴趣浓厚,请你和乐乐一起探究下面问题吧.已知![]() °,射线
°,射线![]() 分别是
分别是![]() 和
和![]() 的平分线;
的平分线;
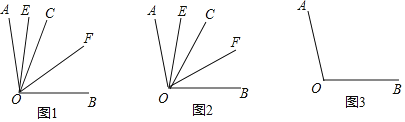
(1)如图1,若射线![]() 在
在![]() 的内部,且
的内部,且![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若射线![]() 在
在![]() 的内部绕点
的内部绕点![]() 旋转,则
旋转,则![]() 的度数为;
的度数为;
(3)若射线![]() 在
在![]() 的外部绕点
的外部绕点![]() 旋转(旋转中
旋转(旋转中![]() ,
,![]() 均指小于
均指小于![]() 的角),其余条件不变,请借助图3探究
的角),其余条件不变,请借助图3探究![]() 的大小,请直接写出
的大小,请直接写出![]() 的度数(不写探究过程)
的度数(不写探究过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:71=7,72=49,73=343,74=2 401,75=16 807,76=117 649,…,那么:71+72+73+…+72 016的末位数字是( )
A. 9B. 7C. 6D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧。为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,点
两点,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
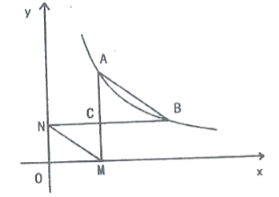
(1)点![]() 的纵坐标为___________;
的纵坐标为___________;
(2)作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连结
,连结![]() .
.
①求证:![]() ;
;
②若四边形![]() 是正方形且面积为
是正方形且面积为![]() ,把直线
,把直线![]() 向右平移
向右平移![]() 个单位,平移后的直线与反比例函数
个单位,平移后的直线与反比例函数![]() 的图象交于
的图象交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲公司单独做需要20天完成,乙公司单独做所用时间是甲公司的1.5倍.
(1)若甲、乙两公司合作完成这项工程需要多少天?
(2)若甲、乙两公司合作完成这项工程,在第10天结束时,甲公司有别的任务,不能继续合作,剩余部分由乙公司单独完成,则乙公司还需要做几天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com