
【题目】如图,△ABC中,∠ABC=90°,AB=BC,D在边 AC上,AE⊥BD于 E
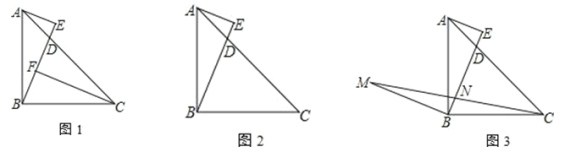
(1)如图1,作 CF⊥BD于F,求证:CF-AE=EF
(2)如图2,若 BC=CD,求![]() 的值
的值
(3)如图3,作 BM⊥BE,且 BM=BE,AE=2,EN=4,连 CM交 BE于 N,请直接写出△BCM的面积为___
【答案】(1)详见解析;(2)![]() ;(3)5
;(3)5
【解析】
(1)利用已知条件易证△ABE≌△BCF,所以CF=BE,AE=BF,进而可证明EF=CF-AE;
(2)作 CF⊥BD于 F,根据(1)可知AE=BF,再根据BC=CD,CF⊥BD得到F为BD中点,故可得到![]() =
=![]() ;
;
(3)过作 CF⊥BD于 F,根据(1)得△ABE≌△BCF,根据BM⊥BE,且 BM=BE得到△BMN≌△FCN,故S△BCM=S△BCF=![]() ×BF×FC,即可求解.
×BF×FC,即可求解.
(1)证明:∵CF⊥BD于点F,AE⊥BD,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
又∵∠ABC=90°,
∴∠ABE+∠CBE=90°,
∴∠BAE=∠CBF,
在三角形ABE和BCF中,
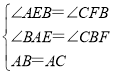 ,
,
∴△ABE≌△BCF(AAS),
∴CF=BE,AE=BF,
∴EF=CF-AE.
(2)如图,作 CF⊥BD于 F,根据(1)可知AE=BF,
∵BC=CD,CF⊥BD
∴F为BD中点,
∴DF=BF=AE
∴![]() =
=![]() ;
;
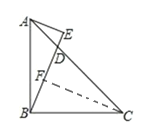
(3)过作CF⊥BD于 F,
由(1)得△ABE≌△BCF,
∵BM⊥BE,且BM=BE,
∴BM=FC
又∠MNB=∠CNF,
∴△BMN≌△FCN,
∴S△BMN=S△FCN,BN=FN
∵AE=2,EN=4,
∴BF= AE=2,BN=![]() BF=1,
BF=1,
故BE=BN+EN=5
故S△BCM=S△BCF=![]() ×BF×FC=
×BF×FC=![]() ×2×BE==5.
×2×BE==5.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
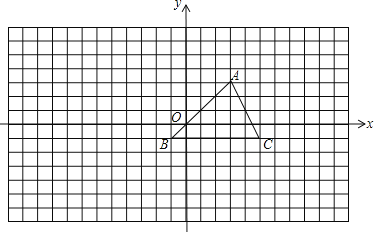
【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() :
:![]() 与抛物线
与抛物线![]() 关于y轴对称, 抛物线
关于y轴对称, 抛物线![]() 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
(1)求b和m的值;
(2)求抛物线![]() 的解析式;
的解析式;
(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线![]() 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
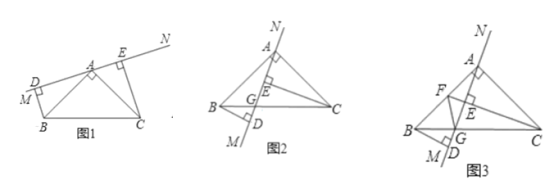
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
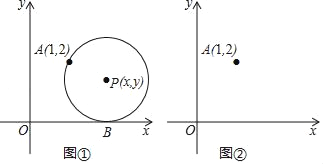
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
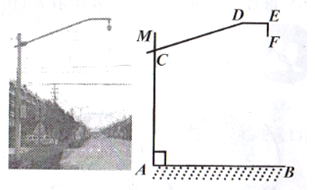
(1)求∠MCD的度数;
(2)求摄像头下端点F到地面AB的距离。(精确到百分位)
(参考数据;sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com