
【题目】乐乐对几何中角平分线的兴趣浓厚,请你和乐乐一起探究下面问题吧.已知![]() °,射线
°,射线![]() 分别是
分别是![]() 和
和![]() 的平分线;
的平分线;
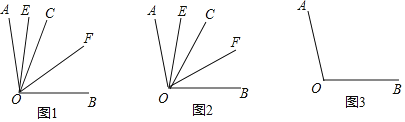
(1)如图1,若射线![]() 在
在![]() 的内部,且
的内部,且![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若射线![]() 在
在![]() 的内部绕点
的内部绕点![]() 旋转,则
旋转,则![]() 的度数为;
的度数为;
(3)若射线![]() 在
在![]() 的外部绕点
的外部绕点![]() 旋转(旋转中
旋转(旋转中![]() ,
,![]() 均指小于
均指小于![]() 的角),其余条件不变,请借助图3探究
的角),其余条件不变,请借助图3探究![]() 的大小,请直接写出
的大小,请直接写出![]() 的度数(不写探究过程)
的度数(不写探究过程)
【答案】(1)50°;(2)50°;(3)50°或130°
【解析】
(1)先求出∠BOC度数,根据角平分线定义求出∠EOC和∠FOC度数,求和即可得出答案;
(2)根据角平分线定义得出∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠EOC+∠FOC=
∠BOC,求出∠EOF=∠EOC+∠FOC=![]() ∠AOB,代入求出即可;
∠AOB,代入求出即可;
(3)分两种情况:①射线OE,OF只有1个在∠AOB外面,根据角平分线定义得出∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠FOC-∠COE=
∠BOC,求出∠EOF=∠FOC-∠COE=![]() ∠AOB;②射线OE,OF,2个都在∠AOB外面,根据角平分线定义得出∠EOF=
∠AOB;②射线OE,OF,2个都在∠AOB外面,根据角平分线定义得出∠EOF=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠EOC+∠COF=
∠BOC,求出∠EOF=∠EOC+∠COF=![]() (360°-∠AOB),代入求出即可.
(360°-∠AOB),代入求出即可.
解:(1)∵∠AOB=100°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=70°,
∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=![]() ∠AOC=15°,∠FOC=
∠AOC=15°,∠FOC=![]() ∠BOC=35°,
∠BOC=35°,
∴∠EOF=∠EOC+∠FOC=15°+35°=50°;
(2)∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC,
∠BOC,
∴∠EOF=∠EOC+∠FOC=![]() ∠AOB=
∠AOB=![]() ×100°=50°;
×100°=50°;
故答案为:50°.
(3)①射线OE,OF只有1个在∠AOB外面,如图3①,
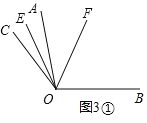
∴∠EOF=∠FOC-∠COE
=![]() ∠BOC-
∠BOC-![]() ∠AOC
∠AOC
=![]() (∠BOC-∠AOC)
(∠BOC-∠AOC)
=![]() ∠AOB
∠AOB
=![]() ×100°=50°;
×100°=50°;
②射线OE,OF2个都在∠AOB外面,如图3②,
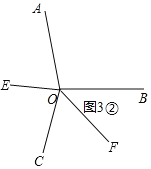
∴∠EOF=∠EOC+∠COF
=![]() ∠AOC+
∠AOC+![]() ∠BOC
∠BOC
=![]() (∠AOC+∠BOC)
(∠AOC+∠BOC)
=![]() (360°-∠AOB)
(360°-∠AOB)
=![]() ×260°=130°.
×260°=130°.
∴∠EOF的度数是50°或130°.


科目:初中数学 来源: 题型:
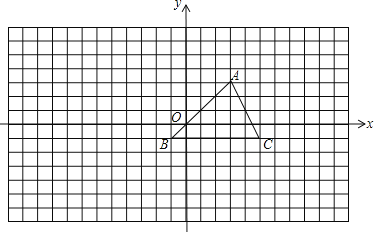
【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() :
:![]() 与抛物线
与抛物线![]() 关于y轴对称, 抛物线
关于y轴对称, 抛物线![]() 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
(1)求b和m的值;
(2)求抛物线![]() 的解析式;
的解析式;
(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线![]() 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
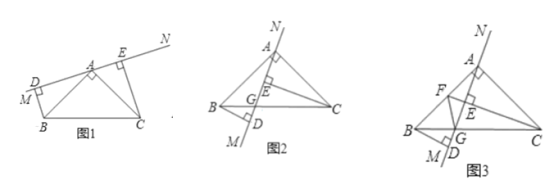
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
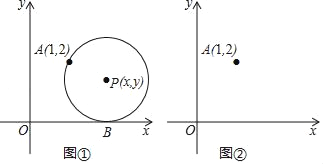
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.
(1)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动.
秒运动.
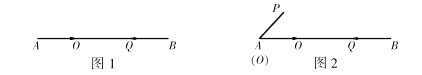
①问经过几秒后![]() 相遇?
相遇?
②几秒钟后![]() 相距
相距![]() ?
?
(2)如图2,![]() ,
,![]() ,点
,点![]() 以每秒
以每秒![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,点
点运动,点![]() 自
自![]() 点向
点向![]() 点运动的同时线段
点运动的同时线段![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转一周停止,假如
顺时针旋转一周停止,假如![]() 两点能相遇,求点
两点能相遇,求点![]() 运动的速度.
运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com