
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
【答案】(1)1;(2)当![]() 秒时,点P到达点A处;(3)
秒时,点P到达点A处;(3)![]() ;(4)当
;(4)当![]() 等于1.5或3.5秒时,P、C之间的距离为2个单位长度.
等于1.5或3.5秒时,P、C之间的距离为2个单位长度.
【解析】
(1)根据题意得到点C是AB的中点;
(2)、(3)根据点P的运动路程和运动速度列出方程;
(4)分两种情况:点P在点C的左边有右边.
1)依题意得,点C是AB的中点,故点C表示的数是:![]() =1.
=1.
故答案是:1;
(2)[6-(-4)]÷2=10÷2=5(秒)
答:当t=5秒时,点P到达点A处.
(3)点P表示的数是2t-4.
故答案是:2t-4;
(4)当点P在点C的左边时,2t=3,则t=1.5;
当点P在点C的右边时,2t=7,则t=3.5.
综上所述,当t等于1.5或3.5秒时,P、C之间的距离为2个单位长度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( )
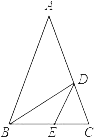
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
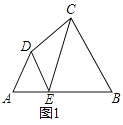
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:

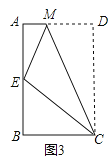
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐对几何中角平分线的兴趣浓厚,请你和乐乐一起探究下面问题吧.已知![]() °,射线
°,射线![]() 分别是
分别是![]() 和
和![]() 的平分线;
的平分线;
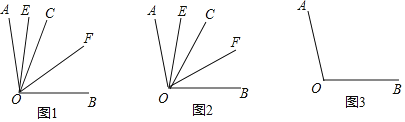
(1)如图1,若射线![]() 在
在![]() 的内部,且
的内部,且![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若射线![]() 在
在![]() 的内部绕点
的内部绕点![]() 旋转,则
旋转,则![]() 的度数为;
的度数为;
(3)若射线![]() 在
在![]() 的外部绕点
的外部绕点![]() 旋转(旋转中
旋转(旋转中![]() ,
,![]() 均指小于
均指小于![]() 的角),其余条件不变,请借助图3探究
的角),其余条件不变,请借助图3探究![]() 的大小,请直接写出
的大小,请直接写出![]() 的度数(不写探究过程)
的度数(不写探究过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如下规律摆放三角形:
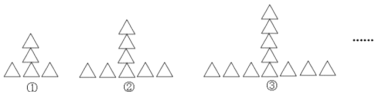
(1)图④中分别有多少个三角形?
(2)按上述规律排列下去,第n个图形中有多少个三角形?
(3)按上述规律排列下去,第2014个图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
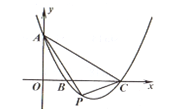
【题目】如图,平面直角坐标系中,抛物线y=-![]() x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A. 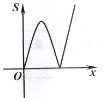 B.
B.  C.
C. 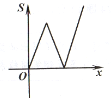 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示数a、b,A、B之间的距离可表示为AB=|a﹣b|.已知数轴上A,B两点分别表示有理数﹣1和x.
(1)若AB=4时,则x的值为 ;
(2)当x=7时,点A,B分别以每秒1个单位长度和2个单位长度的速度同时向数轴负方向运动.求经过多少秒后,点A到原点的距离是点B到原点的距离的2倍;
(3)如图,点A,B,C,D四点在数轴上分别表示的数为﹣4,﹣1,2,6.是否存在点P在数轴上,使得点P到这四点的距离总和的最小?若存在,请直接写点P的位置和距离总和的最小值.若不存在,请说明理由;
![]()
(4)某一直线沿街有2020户民,假定相邻两户居民间隔相同,分别记为a1,a2,a3,a4,a5,…,a2020.某餐饮公司想为这2020户居民提供早餐,决定在路旁建立一个快餐店P.请问点P选在何处,才能使这2020户居民到点P的距离总和最小?试说明原因.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com