
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
【答案】(1)详见解析;(2)结论AM=AD+CM仍然成立;(3)10
【解析】
(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,如图1(1),易证△ADE≌△NCE,从而有AD=CN,只需证明AM=NM即可.
(2)延长AE,BC相交于N,易证△ADE≌△NCE,得AD=CN,AM=MN=NC+MC=AD+MC;.
(3)设MC=x,则BM=BC﹣CN=9﹣x,由(2)知,AM=AD+MC=9+x,在Rt△ABC中,AM2﹣BM2=AB2,即(9+x)2﹣(9﹣x)2=36.
(1)延长AE,BC相交于N,
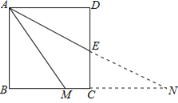
∵四边形ABCD是正方形,∴AD∥BC,∴∠DAE=∠ENC,
∵AE平分∠DAE,∴∠∠DAE=∠MAE,
∴∠ENC=∠MAE,在△ADE和△NCE中,
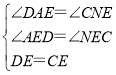 ,
,
∴△ADE≌△NCE,∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(2)结论AM=AD+CM仍然成立,延长AE,BC相交于N,
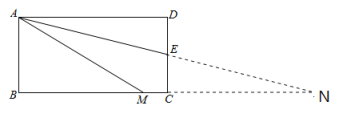
∵四边形ABCD是矩形,∴AD∥BC,∴∠DAE=∠ENC,
∵AE平分∠DAE,∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
在△ADE和△NCE中,,
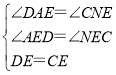
∴△ADE≌△NCE,∴AD=CN,∴AM=MN=NC+MC=AD+MC;
(3)设MC=x,则BM=BC﹣CN=9﹣x,
由(2)知,AM=AD+MC=9+x,在Rt△ABC中,AM2﹣BM2=AB2,
(9+x)2﹣(9﹣x)2=36,
∴x=1,∴AM=AD+MC=10.


科目:初中数学 来源: 题型:
【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, ![]() .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.

【答案】10
【解析】试题分析:根据相似三角形的判定定理得到△ADC∽△BAD,根据相似三角形的面积比等于相似比的平方即可得到结论.
试题解析:∵∠DAB=∠C,∠D=∠D, ∴△ADC∽△BAD,
∴ ,
,
∵△ADC的面积为18cm2 ,
∴△BDA的面积为8cm2 ,
∴△ABC的面积=△ADC的面积﹣△BDA的面积=10cm2
【题型】解答题
【结束】
24
【题目】如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.

查看答案和解析>>
科目:初中数学 来源: 题型:
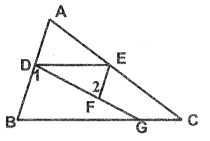
【题目】已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180°( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180°( )
所以 ∥ ( )
所以∠1=∠2( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一股民上星期五买进某公司股票![]() 股,每股
股,每股![]() 元,下表为本周内每日该股票的涨跌情况(单位:元)
元,下表为本周内每日该股票的涨跌情况(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股是________元;
星期三收盘时,每股是________元;
![]() 本周内每股最高价为________元,每股最低价为________元;
本周内每股最高价为________元,每股最低价为________元;
![]() 已知该股民买进股票时付了
已知该股民买进股票时付了![]() ‰的手续费,卖出时还需付成交额
‰的手续费,卖出时还需付成交额![]() ‰的手续费和
‰的手续费和![]() ‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx(k<0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.

【答案】-6
【解析】试题分析:∵点A(x1,y1),B(x2,y2)是双曲线y=![]() 上的点,
上的点,
∴x1y1=x2y2=-3①,
∵直线y=kx(k<0)与双曲线y=![]() 交于点A(x1,y1),B(x2,y2)两点,
交于点A(x1,y1),B(x2,y2)两点,
∴x1=-x2,y1=-y2②,
∴原式=-3x1y1+5x2y2=9-15=-6.
故答案为:-6.
点睛:本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.
【题型】填空题
【结束】
15
【题目】A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了 50%,而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h,则根据题意可列方程为 _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
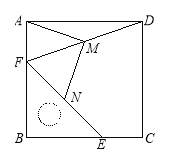
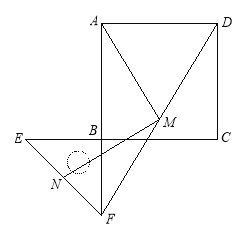
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com