Question

【题目】若数是关于的不等式组至少有个整数解且所有解都是的解，且使关于的分式有整数解．则满足条件的所有整数的个数是（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

根据题意解不等式组，用常数m表示x的解集，通过x的不等式组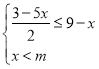至少有3个整数解且所有解都是2x-5≤1的解，确定常数m的取值范围，其次，解分式方程，同样用含有常数m的代数式去表示方程的解，排除掉当解为增根时m的取值，从剩下的整数m的取值中选择使为整数的取值即可．

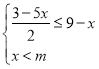
化简得：

∴-5＜x≤m．
又∵2x-5≤1
解得，x≤3．
由不等式组至少有三个整数解且所有解都满足x≤3
故-2≤m≤3．
又∵

整理得，4x-2-（3m-1）=2（x-1）
解得，x=．
由该方程有整数解，则≠1，且3m-1应为2的整数倍．
解得，m≠1．
∴在-2≤m≤3且m≠1中，满足3m-1应为2的倍数的整数m的取值有两个，分别为，-1，3．
故选：D．