
ЁОЬтФПЁПШчЭМЃЌдкЁїADCжаЃЌЕуBЪЧБпDCЩЯЕФвЛЕуЃЌЁЯDAB=ЁЯCЃЌ ![]() ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ

ЁОД№АИЁП10
ЁОНтЮіЁПЪдЬтЗжЮіЃКИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэЕУЕНЁїADCЁзЁїBADЃЌИљОнЯрЫЦШ§НЧаЮЕФУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНМДПЩЕУЕННсТлЃЎ
ЪдЬтНтЮіЃКЁпЁЯDAB=ЁЯCЃЌЁЯD=ЁЯDЃЌ ЁрЁїADCЁзЁїBADЃЌ
Ёр ЃЌ
ЃЌ
ЁпЁїADCЕФУцЛ§ЮЊ18cm2 ЃЌ
ЁрЁїBDAЕФУцЛ§ЮЊ8cm2 ЃЌ
ЁрЁїABCЕФУцЛ§=ЁїADCЕФУцЛ§ЉЁїBDAЕФУцЛ§=10cm2
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
ЁОЬтФПЁПШчЭМЃЌдкЭјИёЭМжаЕФЁїABCгыЁїDEFЪЧЗёГЩЮЛЫЦЭМаЮЃПЫЕУїРэгЩЃЎШчЙћЪЧЃЌЭЌЪБжИГіЫќУЧЕФЮЛЫЦжааФЃЎ

 жЧФмбЕСЗСЗВтПМЯЕСаД№АИ
жЧФмбЕСЗСЗВтПМЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌAB=4ЃЌEЃЌFЗжБ№ЪЧABЁЂBCЕФжаЕуЃЌPЪЧACЩЯвЛЖЏЕуЃЌдђPF+PEЕФзюаЁжЕЪЧЃЈ ЃЉ

A. 3B. ![]() C. 4D.
C. 4D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫСНДЮЭЌЪБдквЛМвСИЕъЙКТђДѓУзЃЌСНДЮДѓУзЕФМлИёЗжБ№ЮЊУПЧЇПЫaдЊКЭbдЊЃЈaЁйbЃЉЃЎМзУПДЮТђ100ЧЇПЫДѓУзЃЌввУПДЮТђ100дЊДѓУзЃЎ
ЃЈ1ЃЉгУКЌaЁЂbЕФДњЪ§ЪНБэЪОЃКМзСНДЮЙКТђДѓУзЙВашИЖПюЁЁ ЁЁдЊЃЌввСНДЮЙВЙКТђЁЁ ЁЁЧЇПЫДѓУзЃЎШєМзСНДЮЙКТђДѓУзЕФЦНОљЕЅМлЮЊУПЧЇПЫQ1дЊЃЌввСНДЮЙКТђДѓУзЕФЦНОљЕЅМлЮЊУПЧЇПЫQ2дЊЃЎдђЃКQ1=ЁЁ ЁЁЃЛQ2=ЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєЙцЖЈЫСНДЮЙКСИЕФЦНОљМлИёЕЭЃЌЫЙКСИЕФЗНЪНОЭИќКЯРэЃЌЧыФуХаЖЯБШНЯМзЁЂввСНШЫЕФЙКСИЗНЪНЃЌФФвЛИіИќКЯРэЃЌВЂЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§![]() КЭ
КЭ![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЧв
ЕФЭМЯѓШчЭМЫљЪОЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉгЩЭМПЩжЊЃЌВЛЕШЪН![]() ЕФНтМЏЪЧ______ЃЛ
ЕФНтМЏЪЧ______ЃЛ
ЃЈ2ЃЉШєВЛЕШЪН![]() ЕФНтМЏЪЧ
ЕФНтМЏЪЧ![]() ЃЎ
ЃЎ
ЂйЕу![]() ЕФзјБъЮЊ______ЃЎ
ЕФзјБъЮЊ______ЃЎ
Ђк![]() ЕФжЕЮЊ_______ЃЎ
ЕФжЕЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЩЯСНЕуЃЌ
ЩЯСНЕуЃЌ![]() ЮЊвЛЖЏЕуЃЌзї
ЮЊвЛЖЏЕуЃЌзї![]() жсЃЌ
жсЃЌ![]() жсЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧ( )
жсЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧ( )

Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂлШє
ЃЛЂлШє![]() ЃЌдђ
ЃЌдђ![]() ЦНЗж
ЦНЗж![]() ЃЛЂмШє
ЃЛЂмШє![]() ЃЌдђ
ЃЌдђ![]()
A. ЂйЂл B. ЂкЂл C. ЂкЂм D. ЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЭМ,ВЂЭъГЩЬюПеЃК
вбжЊжБНЧШ§НЧаЮABC,ЁЯC=90Ёу
(1)Й§ЕуBзїжБЯп1ЦНаагкAC
(2)РћгУГпЙц,ЛГіЯпЖЮACЕФДЙжБЦНЗжЯпEF,НЛABгкЕуE,ACгкЕуF
(3)ЕуAЕНЕуEЕФОрРыЪЧЯпЖЮ ЕФГЄ,ЕуAЕНBCЕФОрРыЪЧЯпЖЮ ЕФГЄЃЌжБЯпLгыACЕФОрРыЪЧЯпЖЮ ЕФГЄ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЧщОГЃЉ
ШчЭМ1ЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌMЪЧBCБпЩЯЕФвЛЕуЃЌEЪЧCDБпЕФжаЕуЃЌAEЦНЗжЁЯDAMЃЎЧѓжЄЃКAM=AD+MCЃЎ

ЃЈЬНОПеЙЪОЃЉ
ЃЈ2ЃЉШєЫФБпаЮABCDЪЧГЄгыПэВЛЯрЕШЕФОиаЮЃЌЦфЫћЬѕМўВЛБфЃЌШчЭМ2ЃЌЪдХаЖЯAM=AD+MCЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјГіжЄУїЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈЭиеЙбгЩьЃЉ
ЃЈ3ЃЉШєЃЈ2ЃЉжаОиаЮABCDСНБпAB=6ЃЌBC=9ЃЌЧѓAMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛдквпЧщЦкМфгУ 3000 дЊЙКНј AЁЂB СНжжПкеж1100 ИіЃЌЙКТђAжжПкежгыЙКТђ B жжПкежЕФЗбгУЯрЭЌЃЌЧвAжжПкежЕФЕЅМлЪЧ B жжПкежЕЅМлЕФ 1.2 БЖЧѓ AЃЌB СНжжПкежЕФЕЅМлИїЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
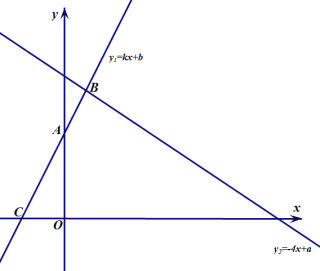
ЁОЬтФПЁПШчЭМЃКдкЪ§жсЩЯAЕуБэЪОЪ§aЃЌBЕуЪОЪ§bЃЌCЕуБэЪОЪ§cЃЌbЪЧзюаЁЕФе§ећЪ§ЃЌЧвaЃЌbТњзу![]() +(cЃ7)2=0ЃЎ
+(cЃ7)2=0ЃЎ
(1) a= ЃЌb= ЃЌc= ЃЎ
(2) ШєНЋЪ§жселЕўЃЌЪЙЕУAЕугыCЕужиКЯЃЌдђЕуBгыЪ§ БэЪОЕФЕужиКЯЃЎ
(3) ЕуAЃЌBЃЌCПЊЪМдкЪ§жсЩЯдЫЖЏЃЌШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ4ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌМйЩшtУыжгЙ§КѓЃЌШєЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЌЕуAгыЕуCжЎМфЕФОрРыБэЪОЮЊACЃЌЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЎдђAB= ЃЌAC= ЃЌBC= ЃЎ(гУКЌtЕФДњЪ§ЪНБэЪО)
(4) ЧыЮЪЃК3BCЃ2ABЕФжЕЪЧЗёЫцзХЪБМфtЕФБфЛЏЖјИФБф? ШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com