
【题目】点A、B在数轴上分别表示数a、b,A、B之间的距离可表示为AB=|a﹣b|.已知数轴上A,B两点分别表示有理数﹣1和x.
(1)若AB=4时,则x的值为 ;
(2)当x=7时,点A,B分别以每秒1个单位长度和2个单位长度的速度同时向数轴负方向运动.求经过多少秒后,点A到原点的距离是点B到原点的距离的2倍;
(3)如图,点A,B,C,D四点在数轴上分别表示的数为﹣4,﹣1,2,6.是否存在点P在数轴上,使得点P到这四点的距离总和的最小?若存在,请直接写点P的位置和距离总和的最小值.若不存在,请说明理由;
![]()
(4)某一直线沿街有2020户民,假定相邻两户居民间隔相同,分别记为a1,a2,a3,a4,a5,…,a2020.某餐饮公司想为这2020户居民提供早餐,决定在路旁建立一个快餐店P.请问点P选在何处,才能使这2020户居民到点P的距离总和最小?试说明原因.
【答案】(1)3或﹣5;(2)经过![]() 秒或5秒后,点A到原点的距离是点B到原点的距离的2倍;(3)点P在B与C之间时,点P到这四点的距离总和的最小,其最小值为13;(4)点P选在a1020与a1011之间,才能使这2020户居民到点P的距离总和最小,理由见解析.
秒或5秒后,点A到原点的距离是点B到原点的距离的2倍;(3)点P在B与C之间时,点P到这四点的距离总和的最小,其最小值为13;(4)点P选在a1020与a1011之间,才能使这2020户居民到点P的距离总和最小,理由见解析.
【解析】
(1)根据距离公式AB=|a﹣b|,分点B在点A左、右两侧两种情况解答即可;
(2)设经过t秒后,点A到原点的距离是点B到原点的距离的2倍,则A点表示的数为(﹣1﹣t),B点表示的数为(7﹣t),然后分点B在原点左右两边,列方程可求得结果;
(3)设P点表示的数为x,分别求出当x<﹣4时,当﹣4≤x<﹣1时,当﹣1≤x<2时,当2≤x<6时,当x≥6时,点P到这四点的距离总和,然后比较求出最小值即可;
(4)根据两点之间的距离,先分析有2户居民点P的位置,有3户居民点P的位置,有4户居民点P的位置,…,最后根据规律可得出有2020户居民点P的位置即可得到结论.
解:(1)∵AB=4,数轴上A,B两点分别表示有理数﹣1和x,
∴当B点在A点右边时,x=﹣1+4=3,
当B点在A点左边时,x=﹣1﹣4=﹣5,
故答案为:3或﹣5;
(2)设经过t秒后,点A到原点的距离是点B到原点的距离的2倍,则A点表示的数为(﹣1﹣t),B点表示的数为(7﹣t),
①当B点在原点右边时,有OA=|﹣1﹣t|=t+1,OB=|7﹣2t|=7﹣2t,则
t+1=2(7﹣2t),
解得,t=![]() ,
,
②当B点在原点左边时,有OA=|﹣1﹣t|=t+1,OB=|7﹣2t|=2t﹣7,则
t+1=2(2t﹣7),
解得,t=5,
综上,t=![]() 或5.
或5.
答:经过![]() 秒或5秒后,点A到原点的距离是点B到原点的距离的2倍;
秒或5秒后,点A到原点的距离是点B到原点的距离的2倍;
(3)设P点表示的数为x,则
当x<﹣4时,距离之和为﹣4﹣x﹣1﹣x+2﹣x+6﹣x=3﹣4x>19,
当﹣4≤x<﹣1时,距离为x+4﹣1﹣x+2﹣x+6﹣x=11﹣2x>13,
当﹣1≤x<2时,距离为x+4+x+1+2﹣x+6﹣x=13,
当2≤x<6时,时,距离为x+4+x+1+x﹣2+6﹣x=9+2x≥13,
当x≥6时,时,距离为x+4+x+1+x﹣2+x﹣6=4x﹣3≥19,
∴当﹣1≤x≤2时,点P到这四点的距离总和的最小,其最小值为13,
即点P在B与C之间时,点P到这四点的距离总和的最小,其最小值为13;
(4)点P选在a1020与a1011之间,才能使这2020户居民到点P的距离总和最小.
理由:若只有a1、a2居民户,P建在a1与a2之间任何一点位置时,2户居民到点P的距离和都为a1与a2间的距离,比建在a1与a2之外小;
若有a1,a2,a3三居民户,P建在a3处时,3户居民到点P的距离和最小,
若有a1,a2,a3,a4四居民户,P建在a2与a3之间任何一点位置时,4户居民到点P的距离和最小,
∴若有a1,a2,a3,a4,a5,…,a20202020户,P建在a1010与a1011之间任何一点位置时,才能使这2020户居民到点P的距离总和最小.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
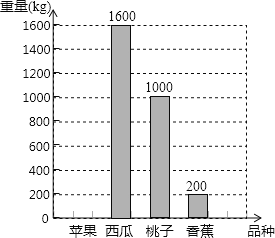
【题目】某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
回答下列问题:
(1)这批水果总重量为 kg;
(2)请将条形图补充完整;
(3)若用扇形图表示统计结果,则桃子所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上。建立平面直角坐标系后,点A的坐标为(4,1),点B的坐标为(1,1).
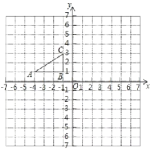
(1)请画出△ABC关于y轴对称的△A1B1C1.
(2)将△ABC绕点O逆时针旋转90°后得到△A2B2C2,试在图中画出图形△A2B2C2,并计算点C旋转到点C2所经过的路径长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每一幅图中都有若干个大小不同的四边形,第1幅图中有1个四边形,第2幅图中有3个四边形,第3幅图中有5个四边形…

(1)第4幅图中有 个四边形,第5幅图中有 个四边形;
(2)根据第1幅图到第5幅图的规律,推测第![]() 幅图中有 个四边形;(用含字母
幅图中有 个四边形;(用含字母![]() 的代数式表示)
的代数式表示)
(3)如果第![]() 幅图中有4039个四边形,请你计算
幅图中有4039个四边形,请你计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
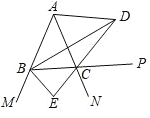
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,![]() ,
,![]() ,则有下列结论:①
,则有下列结论:①![]() ;②点C到EF的距离是2-1;③
;②点C到EF的距离是2-1;③![]() 的周长为2;④
的周长为2;④![]() ,其中正确的结论有( )
,其中正确的结论有( )
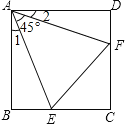
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
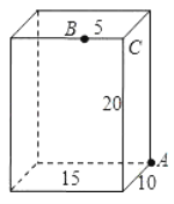
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com