
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,点
两点,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
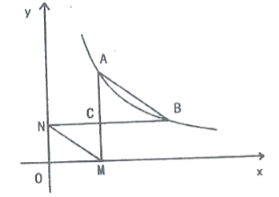
(1)点![]() 的纵坐标为___________;
的纵坐标为___________;
(2)作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连结
,连结![]() .
.
①求证:![]() ;
;
②若四边形![]() 是正方形且面积为
是正方形且面积为![]() ,把直线
,把直线![]() 向右平移
向右平移![]() 个单位,平移后的直线与反比例函数
个单位,平移后的直线与反比例函数![]() 的图象交于
的图象交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,求
点,求![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)16
;(2)证明见解析;(3)16
【解析】
(1)由点A的横坐标,利用反比例函数图象上点的坐标特征可求出点A的纵坐标
(2)①由反比例函数图象上点的坐标特征可得出点A,B的坐标,进而可得出MC,NC,BC,AC的长度,由长度之间的关系可得出![]() ,结合∠ACB=∠MCN=90°可证出△ACB∽△MCN,利用相似三角形的性质可得出∠ABC=∠MNC,再利用“内错角相等,两直线平行”可证出AB∥MN
,结合∠ACB=∠MCN=90°可证出△ACB∽△MCN,利用相似三角形的性质可得出∠ABC=∠MNC,再利用“内错角相等,两直线平行”可证出AB∥MN
②由正方形的性质结合反比例函数图象上点的坐标特征,可得出点A,C的坐标及k值,由点C的坐标可得出直线OC的解析式,利用平移的性质可求出直线PQ的解析式及点Q的坐标,联立直线PQ和反比例函数解析式成方程组,通过解方程组可求出点P的坐标,再利用两点间的距离公式可求出![]() 的值
的值
解:(1)当![]() 时,
时,![]() ,
,
∴点A的纵坐标为![]() ,
,
故答案为:![]()
(2)①证明:当![]() 时,
时,![]() ,
,
∴点B的坐标为![]()
∵AM⊥x轴,BN⊥y轴
∴点C的坐标为![]() ,
,
∴NC=m,BC=n-m,MC=![]() ,AC=
,AC=![]() ,
,
∴![]() ,
,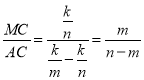 ;
;
∴![]()
又∵∠ACB=∠MCN=90°
∴△ACB∽△MCN
∴∠ABC=∠MNC
∴AB∥MN
②∵四边形ABMN是正方形,
∴CM=CN, BN=2CN, AM=2CM
∴n=2m,△CMN为等腰直角三角形
∵![]()
∴![]()
∴CM=CN=2
∴m=2,n=4
∴点A的坐标为(2,4),点C的坐标为(2,2)
∴k=2×4=8,直线OC的解析式为y=x.
∵把直线OC向右平移c个单位得到直线PQ
∴直线PQ的解析式为y=x-c,点Q的坐标为(c,0)
联立直线PQ和反比例函数解析式成方程组得: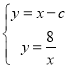 ,
,
解得: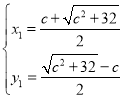 ,
, 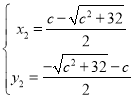 (舍去)
(舍去)
∴点P的坐标为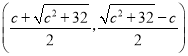
∴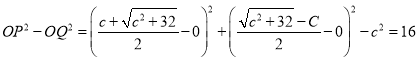
故答案为:16


科目:初中数学 来源: 题型:
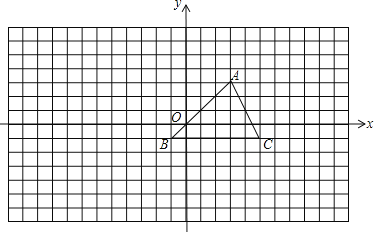
【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
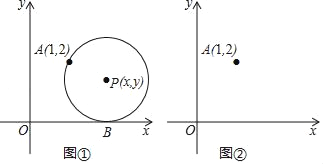
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.
(1)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动.
秒运动.
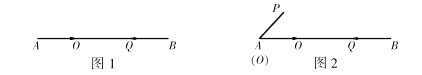
①问经过几秒后![]() 相遇?
相遇?
②几秒钟后![]() 相距
相距![]() ?
?
(2)如图2,![]() ,
,![]() ,点
,点![]() 以每秒
以每秒![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,点
点运动,点![]() 自
自![]() 点向
点向![]() 点运动的同时线段
点运动的同时线段![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转一周停止,假如
顺时针旋转一周停止,假如![]() 两点能相遇,求点
两点能相遇,求点![]() 运动的速度.
运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
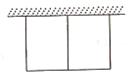
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
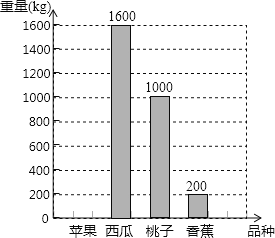
【题目】某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
回答下列问题:
(1)这批水果总重量为 kg;
(2)请将条形图补充完整;
(3)若用扇形图表示统计结果,则桃子所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
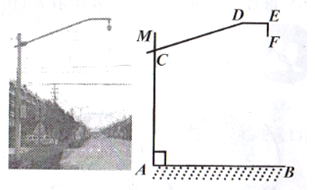
(1)求∠MCD的度数;
(2)求摄像头下端点F到地面AB的距离。(精确到百分位)
(参考数据;sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是____.

①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com