
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣4,0),
B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.
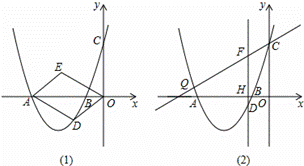
①如图(1),若四边形ODAE是以OA为对角线的平行四边形,当平行四边形
ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
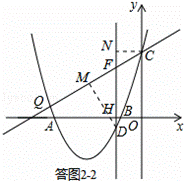
②如图(2),直线y=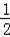 x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x
x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x
轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与
点C到直线DF的距离之比为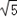 :2?若存在,请求出点D的坐标;若不存在,
:2?若存在,请求出点D的坐标;若不存在,
请说明理由.
解:(1)把点A(﹣4,0),B(﹣1,0)代入解析式y=ax2+bx+3,
得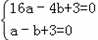 ,解得
,解得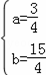 ,
,
∴抛物线的解析式为:y=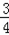 x2+
x2+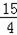 x+3. 5分
x+3. 5分
(2)①如图2﹣1,过点D作DH⊥x轴于点H.
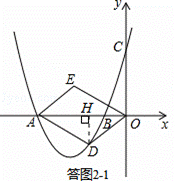
∵S▱ODAE=6,OA=4,
∴S△AOD=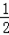 OA•DH=3,
OA•DH=3,
∴DH=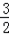 .
.
因为D在第三象限,所以D的纵坐标为负,且D在抛物线上,
∴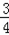 x2+
x2+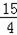 x+3=﹣
x+3=﹣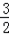 ,
,
解得:x1=﹣2,x2=﹣3. 
∴点D坐标为(﹣2,﹣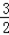 )或(﹣3,﹣
)或(﹣3,﹣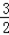 ). 8分
). 8分
当点D为(﹣2,﹣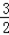 )时,DH垂直平分OA,平行四边形ODAE为菱形;
)时,DH垂直平分OA,平行四边形ODAE为菱形;
当点D为(﹣3,﹣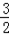 )时,OD≠AD,平行四边形ODAE不为菱形.10分
)时,OD≠AD,平行四边形ODAE不为菱形.10分
②假设存在.
如图2﹣2,过点D作DM⊥CQ于M,过点C作CN⊥DF于N,
则DM:CN= :2.
:2.
设D(m,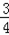 m2+
m2+ m+3)(m<0),则F(m,
m+3)(m<0),则F(m,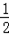 m+3).
m+3).
∴CN=﹣m,NF=﹣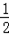 m
m
∴CF=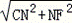 =﹣
=﹣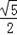 m.
m.
∵∠DMF=∠CNF=90°,∠DFM=∠CFN,
∴△DMF∽△CNF,
∴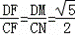 ,
,
∴DF=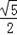 CF=﹣
CF=﹣ m.
m.
∴DN=NF+DF=﹣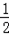 m﹣
m﹣ m=﹣
m=﹣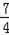 m.
m.
又DN=3﹣(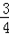 m2+
m2+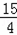 m+3)=﹣
m+3)=﹣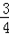 m2﹣
m2﹣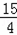 m,
m,
∴﹣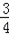 m2﹣
m2﹣ m=﹣
m=﹣ m
m
解得:m=﹣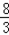 或m=0(舍去)
或m=0(舍去)
∴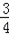 m2+
m2+ m+3=﹣
m+3=﹣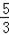
∴D(﹣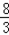 ,﹣
,﹣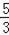 ).
).
综上所述,存在满足条件的点D,点D的坐标为(﹣ ,﹣
,﹣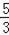 )
)


科目:初中数学 来源: 题型:
我市为治理污水,某地需要铺设一段全长为300 m的污水排放管道.铺设120 m后,为了尽量减少施工对我市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.求原计划每天铺设管道的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
九年一班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行
了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,
如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点
离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高
度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰
角为60°,求旗杆AE的高度(精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
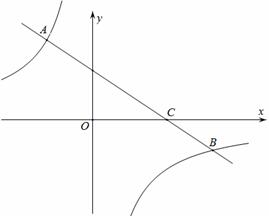
如图,一次函数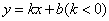 的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
(1)求该一次函数的解析式;
(2)若反比例函数 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求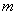 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com