
 如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.
如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.分析 (1)根据等高的三角形面积的比等于底的比求得三角形ADC的面积和三角形ABD的面积,然后根据三角形的中线把三角形分成两个面积相等的三角形即可求得△CDE的面积;
(2)求得三角形BCE的面积,然后根据三角形的中线把三角形分成两个面积相等的三角形即可求得△BEF的面积.
解答 解:(1)∵△ABD和△ADC不等底等高,BD:CD=2:3,
∴S△ABD=$\frac{2}{5}$S△ABC=8,S△ADC=20-8=12,
∵点E是AD的中点,
∴S△CDE=$\frac{1}{2}$S△ADC=$\frac{1}{2}$×12=6(cm2);
(2)∵S△BDE=$\frac{1}{2}$S△ABD=$\frac{1}{2}$×8=4
∴S△BCE=S△BDE+S△DCE=6+4=10,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×10=5(cm2).
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
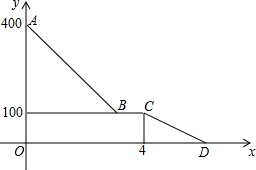 小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com