
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
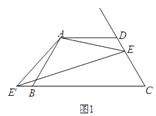
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
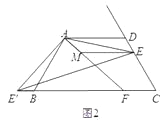
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
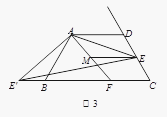
【答案】(1)∠AEE'=30°;
(2)当点E在线段CD上时,![]() ;
;
当点E在CD的延长线上时,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
(3)![]() .
.
【解析】
试题(1)根据旋转地的性质易得到△ADE≌△ABE/,∠EAE/=120°,所以∠AEE/=30°.
由于点E是射线CD上一动点,其位置不确定,故应分情况讨论:一是当点E在线段CD上时:此时易得![]() ;二是点E在CD的延长线上时,仍需考虑多种情况,可以知道,当∠EAD=300时,AE旋转后的直线与BC平行,当∠EAD=900时,AE旋转后的直线与AB共线,而∠EAD不可能为1200,所以应再次细分为三种情况:即当
;二是点E在CD的延长线上时,仍需考虑多种情况,可以知道,当∠EAD=300时,AE旋转后的直线与BC平行,当∠EAD=900时,AE旋转后的直线与AB共线,而∠EAD不可能为1200,所以应再次细分为三种情况:即当![]() 时;当
时;当![]() 时;当
时;当![]() 时.
时.
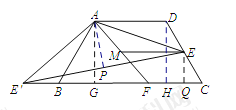
(3)如图,作![]() 于点G, 作
于点G, 作![]() 于点H.易知四边形AGHD是矩形和两个全等的直角三角形
于点H.易知四边形AGHD是矩形和两个全等的直角三角形![]() ;∴点
;∴点![]() 、B、C在一条直线上.继续作
、B、C在一条直线上.继续作![]() 于Q.
于Q.![]() 于点P. 多次利用勾股定理可得
于点P. 多次利用勾股定理可得![]() ,
,![]() ,
,![]() ;继而证明Rt△AG E'∽Rt△FA E',根据相似三角形性质可求解.
;继而证明Rt△AG E'∽Rt△FA E',根据相似三角形性质可求解.
试题解析:
解:(1) 30°.
当点E在线段CD上时,![]() ;
;
当点E在CD的延长线上,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
(3)作![]() 于点G, 作
于点G, 作![]() 于点H.
于点H.
由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°,
易知四边形AGHD是矩形和两个全等的直角三角形![]() .则GH="AD" , BG=CH.
.则GH="AD" , BG=CH.
∵![]() ,
,
∴点![]() 、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=
、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=![]() ,.
,.
作![]() 于Q.在Rt△EQC中,CE="2,"
于Q.在Rt△EQC中,CE="2,"![]() ,
,
∴![]() ,
,![]() .
.
∴E'Q=![]() .
.
作![]() 于点P.
于点P.
∵△ADE绕点A顺时针旋转120°后,得到△ABE'.
∴△A EE'是等腰三角形,![]() .
.
∴在Rt△AP E'中,E'P=![]() .
.
∴EE'="2" E'P=![]() .
.
∴在Rt△EQ E'中,E'Q=![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]()
在Rt△E'AF中,![]()
∴Rt△AG E'∽Rt△FA E'.
∴![]()
∴![]() .
.
∴![]() .
.
由(2)知:![]() .
.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
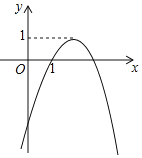
【题目】如图,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,①abc<0,②2a+b>0,③a-b+c<0,④b2>4ac,⑤关于x的方程ax2+bx+c-2=0没有实数根.则下列结论正确的有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是 ( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆![]() 的直径
的直径![]() ,形如三角板的
,形如三角板的![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上,设运动时间为
上,设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________,当
________,当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________;
________;
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?

查看答案和解析>>
科目:初中数学 来源: 题型:
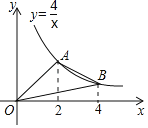
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com