练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有一个渔具包，包内装有A，B两只鱼竿，长度分别为3.6m，4.5m，包内还装有绑好鱼钩的a1 ， a2 ， b三根钓鱼线，长度分别为3.6m，3.6m，4.5m．若从包内随即取出一支鱼竿，再随即取出一根钓鱼线，则鱼竿和鱼钩线长度相同的概率是多少？（请画树状图或列表说明）

    【答案】解：画树状图得： ∵共有6种等可能的结果，鱼竿和鱼钩线长度相同的有：（A，a1），（A，a2），（B，b），
    ∴鱼竿和鱼钩线长度相同的概率是： = ．

    【解析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与鱼竿和鱼钩线长度相同的情况，然后利用概率公式求解即可求得答案．
    【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识，掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明有2件上衣，分别为红色和蓝色，有3条裤子，其中2条为蓝色、1条为棕色．小明任意拿出1件上衣和1条裤子穿上．请用画树状图或列表的方法列出所有可能出现的结果，并求小明穿的上衣和裤子恰好都是蓝色的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在点A′、D′处，且A′D′经过点B，EF为折痕，当D′F⊥CD时， 的值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”，为了了解某学校九年级学生此项目平时的训练情况，随机抽取了该校部分九年级学生进行测试，根据测试结果，制作了如下尚不完整的频数分布表：

    组别

    垫球个数x（个）

    频数（人数）

    频率

    1

    10≤x＜20

    5

    0.10

    2

    20≤x＜30

    a

    0.18

    3

    30≤x＜40

    20

    b

    4

    40≤x＜50

    16

    0.32

    合计

    1


    （1）表中a= ， b=；
    （2）这个样本数据的中位数在第组；
    （3）下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准，若该校九年级有500名学生，请你估计该校九年级学生在这一项目中得分在7分以上（包括7分）学生约有多少人？ 排球30秒对墙垫球的中考评分标准

    分值

    10

    9

    8

    7

    6

    5

    4

    3

    2

    1

    排球（个）

    40

    36

    33

    30

    27

    23

    19

    15

    11

    7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3，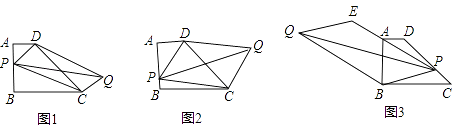
    问题1：如图1，P为AB边上的一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？
    问题2：如图2，若P为AB边上一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
    问题3：若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
    问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE=nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解 如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
    探究发现

    （1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？（填“是”或“不是”）．
    （2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 应用提升
    （3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角． 请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的口袋里装有白、红、黑三种颜色的小球，其中白球2只，红球1只，黑球1只，它们除了颜色之外没有其它区别，从袋中随机地摸出1只球，记录下颜色后放回搅匀，再摸出第二只球并记录颜色，求两次都摸出白球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．
    （1）求证：△BDQ≌△ADP；
    （2）已知AD=3，AP=2，求cos∠BPQ的值（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a，b，c为常数且a≠0）的图象如图所示，则一次函数y=ax+b与反比例函数y= 的图象可能是（ ）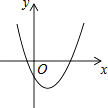
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案