练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在函数y=$\frac{\sqrt{x-1}}{2-x}$中，自变量x的取值范围是x≥1且x≠2．

    分析 根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，就可以求解．

    解答 解：根据二次根式有意义，分式有意义得：x-1≥0且2-x≠0，
    解得：x≥1且x≠2．
    故答案为x≥1且x≠2．

    点评 本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．面积为120cm2的直角三角形，它的一条直角边为10cm，那么它的斜边长为6$\sqrt{10}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．为了培养学生的阅读习惯，某校开展了“读好书，助成长”系列活动，并准备购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，根据统计图所提供的信息，回答下列问题：
    （1）本次调查共抽查了120名学生；
    （2）两幅统计图中的m=48，n=15；
    （3）已知该校共有960名学生，请估计该校喜欢阅读“A”类图书的学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

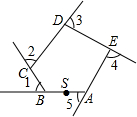    17．如图，五边形ABCDE是一块草地．小明从点S出发，沿着这个五边形的边步行一周，最后仍回到起点S处，小明在各拐弯处转过的角度之和是360°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

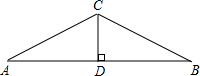    4．如图，要焊接一个等腰三角形钢架，钢架的底角为35°，高CD长为3米，则斜梁AC的长为（　　）米．
    A．$\frac{3}{cos35°}$B．$\frac{3}{tan35°}$C．3sin35°D．$\frac{3}{sin35°}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求代数式$\frac{a+1}{a-2}$÷（a+2-$\frac{3}{2-a}$）的值，其中a=tan45°+2sin60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．在圆中，30°的圆周角所对的弦的长度为$\sqrt{3}$，则这个圆的半径是$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．长珲高铁于2015年9月20日全线开通，从吉林经图们至珲春线路的全长为360公里，360这个数用科学记数法表示为（　　）
    A．0.36×102B．0.36×103C．3.6×102D．3.6×103

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．问题情境：
    我们知道若一个矩形的周长固定，当相邻两边相等，即为正方形时，面积是最大的，反过来，若一个矩形的面积固定，它的周长是否会有最值呢？
    探究方法：
    用两条直角边分别为a、b的四个全等的直角三角形，可以拼成一个正方形，若a≠b，可以拼成如图①的正方形，从而得到a2+b2＞4×$\frac{1}{2}$ab，即a2+b2＞2ab；若a=b，可以拼成如图②的正方形，从而得到a2+b2=4×$\frac{1}{2}$ab，即a2+b2=2ab．
    于是我们可以得到结论：a，b为正数，总有a2+b2≥2ab，且当a=b时，代数式a2+b2取得最小值为2ab．
    另外，我们也可以通过代数式运算得到类似上面的结论．
    ∵（a-b）2=a2-2ab+b2≥0，a2+b2≥2ab，∴对于任意实数a，b，总有a2+b2≥2ab，且当a=b时，代数式a2+b2取得最小值为2ab．
    仿照上面的方法，对于正数a，b试比较a+b和2$\sqrt{ab}$的大小关系．
    类比应用
    利用上面所得到的结论，完成填空：
    （1）当x＞0时，x2+$\frac{1}{{x}^{2}}$≥2x•$\frac{1}{x}$，代数式x2+$\frac{1}{{x}^{2}}$有最小值为2．
    （2）当x＞0时，x+$\frac{9}{x}$≥2$\sqrt{x•\frac{9}{x}}$，代数式x+$\frac{9}{x}$有最小值为6．
    （3）当x＞2时，x+$\frac{5}{x-2}$≥2$\sqrt{（x-2）•\frac{5}{x-2}}$+2，代数式x+$\frac{5}{x-2}$有最小值为2$\sqrt{5}$+2．
    问题解决：
    若一个矩形的面积固定为n，它的周长是否会有最值呢？若有，求出周长的最值及此时矩形的长和宽；若没有，请说明理由，由此你能得到怎样的结论？

    查看答案和解析>>

    同步练习册答案