
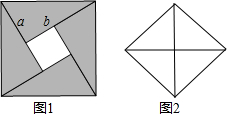
 问题情境:
问题情境:分析 探究方法:仿照给定的方法,即可得出a+b≥2$\sqrt{ab}$这一结论;
类比应用:(1)根据探究方法中的结论,代入数据即可得出结论;
(2)根据探究方法中的结论,代入数据即可得出结论;
(3)代数式中先-2再+2,根据探究方法中的结论,代入数据即可得出结论;
问题解决:设该矩形的长为a,宽为b(a≥b>0),根据a+b≥2$\sqrt{ab}$,结合矩形的周长和面积公式,即可得出结论.
解答 解:探究方法:
∵当a,b均为正数时,$(\sqrt{a}-\sqrt{b})^{2}$=a+b-2$\sqrt{ab}$≥0,
∴a+b≥2$\sqrt{ab}$.
类比应用:
(1)结合探究方法中得出的结论可知:
x2+$\frac{1}{{x}^{2}}$≥2x•$\frac{1}{x}$=2,代数式x2+$\frac{1}{{x}^{2}}$有最小值为2.
故答案为:2x•$\frac{1}{x}$;小;2.
(2)结合探究方法中得出的结论可知:
当x>0时,x+$\frac{9}{x}$≥2$\sqrt{x•\frac{9}{x}}$=6,代数式x+$\frac{9}{x}$有最小值为6.
故答案为:2$\sqrt{x•\frac{9}{x}}$;小;6.
(3)结合探究方法中得出的结论可知:
当x>2时,x+$\frac{5}{x-2}$≥2$\sqrt{(x-2)•\frac{5}{x-2}}$+2=2$\sqrt{5}$+2,代数式x+$\frac{5}{x-2}$有最小值为2$\sqrt{5}$+2.
故答案为:2$\sqrt{(x-2)•\frac{5}{x-2}}$+2;小;2$\sqrt{5}$+2.
问题解决:
设该矩形的长为a,宽为b(a≥b>0),
根据题意知:周长C=2(a+b)≥4$\sqrt{ab}$=4$\sqrt{n}$,且当a=b时,代数式2(a+b)取得最小值为4$\sqrt{n}$,
此时a=b=$\sqrt{n}$.
故若一个矩形的面积固定为n,它的周长是有最小值,周长的最小值为4$\sqrt{n}$,此时矩形的长和宽均为$\sqrt{n}$.
点评 本题考查了矩形的面积公式、矩形的周长公式以及完全平方式的展开式,解题的关键:(探究方法)仿照给定方法套入数据;(类比应用)结合前面得出的结论套入数据;(问题解决)利用前面结论找出周长的最值.本题属于中档题,难度不大,由于本题篇幅较长,孩子们很难耐下心来细读,其实像这样的阅读形题,只要读懂题意仿照例题给定方法,套入数据即可得出结论,为此应加强这方面的练习.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 67.7×1012 | B. | 6.77×1013 | C. | 0.677×1014 | D. | 6.77×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 同旁内角相等,两直线平行 | |
| C. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
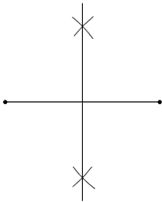 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )| A. | 尺规作线段的垂直平分线 | B. | 尺规作一条线段等于已知线段 | ||
| C. | 尺规作一个角等于已知角 | D. | 尺规作角的平分线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com