
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:选择题
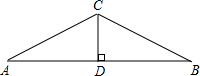 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.
如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.| A. | $\frac{3}{cos35°}$ | B. | $\frac{3}{tan35°}$ | C. | 3sin35° | D. | $\frac{3}{sin35°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
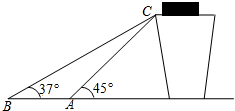 某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)
某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
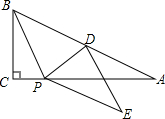 在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.
在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
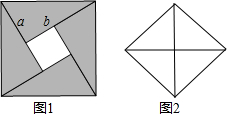 问题情境:
问题情境:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),B(4,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A地 | B地 | C地 | 合计 | |
| 水蜜桃质量(吨) | x | 20-3x | 2x | 20 |
| 运费(元) | 300x | 80(20-3x) | 500x | 560x+1600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com