
| A地 | B地 | C地 | 合计 | |
| 水蜜桃质量(吨) | x | 20-3x | 2x | 20 |
| 运费(元) | 300x | 80(20-3x) | 500x | 560x+1600 |
分析 (1)①根据运往B地的产品吨数=总吨数-运往A地的产品吨数-运往C地的产品吨数;B地运费=总运费-A地运费-C地运费,即可补全图表;
②根据运往B地的吨数不多于运往A地的吨数,总运费不超过5520元列出不等式组,求出x的取值范围,再根据x只能取整数,即可得出运输方案;
(2)总运费=A产品的运费+B产品的运费+C产品的运费,进而根据函数的增减性再求出x的范围即可求出n的最小值.
解答 解:(1)①运往C地的产品吨数=2x,运往B地的产品吨数=总吨数-运往A地的产品吨数-运往C地的产品吨数=(20-3x)吨.
B地运费=总运费-A地运费-C地运费=560x+1600-800x=80(20-3x).
故答案分别为20-3x,2x,80(20-3x).
②由题意得$\left\{\begin{array}{l}{20-3x≤x}\\{560x+1600≤5520}\end{array}\right.$,解得5≤x≤7,
∵x是整数,
∴x=5或6或7.x=7不合题意舍弃
有两种方案,分别是(i)A地5吨,B地5吨,C地10吨;(ii)A地6吨,B地2吨,C地12吨;
(2)由题意:300x+80(n-3x)+500x=7360,
整理得7x+n=92,
∴n=92-7x,
∵n-3x>0,
∴92-7x-3x>0,
∴x<9.2,
∵x是整数,
∴x=9时,n最小值=92-63=29.
点评 考查一元一次不等式组的应用,解题的关键是理解题意,认真读懂表格信息,难点是运费条件在表格中得到,第二个问题中自变量x的范围的确定也是难点,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则| A. | ①③ | B. | ②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:
我国宣布划设东海防空识别区如图所示,具体范围为六点连线与我领海线之间空域.其A、B、C三点的坐标数据如表:| A | B | C | |
| 北纬(度) | 31°00′ | 33°11′ | 25°38′ |
| 东经(度) | 128°20′ | 125°00′ | 125°00′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
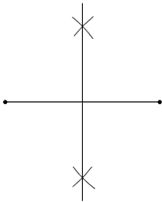 如图所示的尺规作图的痕迹表示的是( )
如图所示的尺规作图的痕迹表示的是( )| A. | 尺规作线段的垂直平分线 | B. | 尺规作一条线段等于已知线段 | ||
| C. | 尺规作一个角等于已知角 | D. | 尺规作角的平分线 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com