Question

10．已知，直线AP是过正方形ABCD顶点A的任一条直线（不过B、C、D三点），点B关于直线AP的对称点为E，连结AE、BE、DE，直线DE交直线AP于点F．

（1）如图1，直线AP与边BC相交．
①若∠PAB=20°，则∠ADF=65°，∠BEF=45°；
②请用等式表示线段AB、DF、EF之间的数量关系，并说明理由；
（2）如图2，直线AP在正方形ABCD的外部，且$DF=6\sqrt{2}$，$EF=8\sqrt{2}$，求线段AF的长．

Answer 1

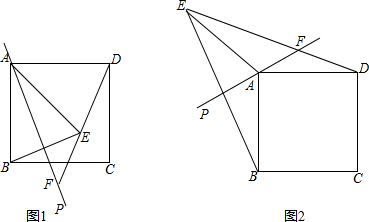
分析 （1）①利用轴对称的性质以及等腰三角形的性质得出即可；②连接BD，BF先依据翻折的性质证明△BEF为等腰直角三角形，从而得到△BFD为直角三角形，由勾股定理可得到BF、FD、BD之间的关系，然后由△ABD为等腰直角三角形，从而得打BD与AB之间的关系，故此可得到BF、FD、AB之间的关系
（2）连接BF、DB．先依据翻折的性质和等腰三角形的性质证明∠BFD=90°，然后在△BDF中，由勾股定理可求得BD的长，从而求得AB的长，然后在等腰直角三角形EFB中可求得FG=GB=8，然后再Rt△AGB中，由勾股定理可求得AG的长，由AF=FG-AG可求得AG的长．

解答 解：（1）①翻折的性质可知：∠PAB=∠PAE=20°，AE=AB．
∴∠AEB=∠ABE=$\frac{1}{2}$×（180°-40°）=70°．
∵ABCD为正方形，
∴AB=AD，∠BAD=90°．
∴AE=AD，∠DAE=50°．
∴∠ADE=∠AED=$\frac{1}{2}$×（180°-50°）=65°．
∴∠BEF=180°-70°-65°=45°．
故答案为：65；45．
②线段AB、DF、EF之间的数量关系是：EF²+DF²=2AB²．
理由：连接BD，BF．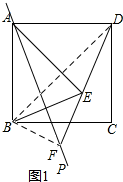

∵由翻折的性质可知：BF=FE，
∴∠FBE=∠FEB=45°．
∴∠BFE=90°．
∴BF²+DF²=DB²．
∵BD=$\sqrt{2}$AB，
∴BD²=2AB²．
∴EF²+DF²=2AB²．
（2）如图2所示：连接BF、DB．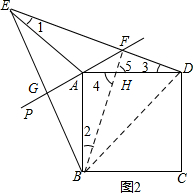

由翻折的性质可知：AB=AE，∠1=∠2，EF=BF=8$\sqrt{2}$，EG=GB．
又∵AD=AB，
∴AE=AD．
∴∠1=∠3．
∴∠2=∠3．
∵∠4=∠5，
∴∠5+∠3=∠2+∠4=90°．
∴△FDB和△EFB均为直角三角形，
∴BD=$\sqrt{F{D}^{2}+B{F}^{2}}$=10$\sqrt{2}$．
∴AB=$\frac{\sqrt{2}}{2}$BD=10$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10．
∵在Rt△EFB中，EF=BF，
∴EB=$\sqrt{2}$EF=$\sqrt{2}$×8$\sqrt{2}$=16．
∴GF=EG=BG=8．
在Rt△ABG中，AG=$\sqrt{A{B}^{2}-P{B}^{2}}$=6．
∴AF=FG-AG=8-6=2．

点评 本题主要考查的是四边形的综合应用，解答本题主要应用了翻折的性质、正方形的性质、勾股定理、等腰直角三角形的性质、等腰三角形的性质、三角形的内角和定理，证得△BFD是直角三角形是解题的关键．