
 ��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����B��4��1����
��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����B��4��1�������� ��1������A��B��������������ߵĽ���ʽ�õ�����m��n�ķ����飬�Ӷ������m��n��
��2������B��BH��OH������õ�C�����꣬Ȼ����֤����AOC�͡�BHCΪ����ֱ�������Σ��Ӷ�����á�ACB=90�㣬Ȼ�����ݹ��ɶ��������AC��BC�ij����������������Ǻ����Ķ������ô𰸣�
��3������P��PG��OA����G�ڵ�A���·�ʱ����Ϊ��PAQ=��CAB�͡�PAQ=��CBA�������������G�ڵ�A���Ϸ�����Ϊ��PAQ=��CAB�͡�PAQ=��CBA�����������㼴�ɣ�
��� �⣺��1���߰�A��0��3����B��4��1������y=$\frac{1}{2}$x2+mx+n��$\left\{\begin{array}{l}{n=3}\\{8+4m+n=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{n=3}\\{m=-\frac{5}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{5}{2}$x+3��
��2������B��BH��x����H����ͼ1��
����y=0���ã�$\frac{1}{2}$x2-$\frac{5}{2}$x+3=0����ã�x1=2��x2=3��
���C��������3��0����
��B��4��1����
��BH=1��OC=3��OH=4��CH=4-3=1��
��BH=CH=1��
�ߡ�BHC=90�㣬
���BCH=45�㣬BC=$\sqrt{2}$��
ͬ������ACO=45�㣬AC=3$\sqrt{2}$��
���ACB=180��-45��-45��=90�㣬
��tan��BAC=$\frac{BC}{AC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$��
��3�����ڵ�P��ʹ����A��P��QΪ��������������ACB���ƣ�
����P��PG��y����G�����PGA=90�㣮
���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG=x��
��PQ��PA����ACB=90�㣬
���APQ=��ACB=90�㣮
����ͼ2�٣�����PAQ=��CABʱ��
�ߡ�PGA=��ACB=90�㣬��PAQ=��CAB��
���PGA�ס�BCA��
��$\frac{PG}{AG}=\frac{BC}{AC}$=$\frac{1}{3}$��
��AG=3PG=3x��
��P��x��3-3x����
��P��x��3-3x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3����$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3-3x��
�����ã�x2+x=0
��ã�x1=0����ȥ����x2=-1����ȥ����
����ͼ2�ڣ�����PAQ=��CBAʱ������P��PG��y�ᣬ����ΪG��
�ߡ�PAG=��CBA����PGA=��ACB=90�㣬
���PAG�ס�CBA��
ͬ���ɵã�AG=$\frac{1}{3}$PG=$\frac{1}{3}$x����P��x��3-$\frac{1}{3}$x����
��P��x��3-$\frac{1}{3}$x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3����$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3-$\frac{1}{3}$x��
�����ã�x2-$\frac{13}{3}$x=0
��ã�x1=0����ȥ����x2=$\frac{13}{3}$��
��P��$\frac{13}{3}$��$\frac{14}{9}$����
��ͼ����ʾ������PAQ=��CABʱ������P��PG��y����ΪG��
�ۡߡ�PAG=��CAB����PGA=��ACB��
���PAG�ס�CAB��
��$\frac{PG}{AG}=\frac{BC}{AC}=\frac{1}{3}$��
��AG=3PG=3x��
��P��x��3+3x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3����$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3+3x��
�����ã�$\frac{1}{2}$x2-$\frac{11}{2}x$=0��
��ã�x1=0����ȥ����x2=11��
��P��11��36����
����ͼ����ʾ������PAQ=��CBAʱ������P��PG��OA������ΪG��
�ߡ�PAG=��CBA����PGA=��ACB=90�㣬
���PAG�ס�CBA��
ͬ���ɵã�AG=$\frac{1}{3}$PG=$\frac{1}{3}$x����P��x��3+$\frac{1}{3}$x����
��P��x��3+$\frac{1}{3}$x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3����$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3+$\frac{1}{3}$x�������ã�$\frac{1}{2}$x2$-\frac{17}{6}$x=0��
��ã�x1=0����ȥ����x2=$\frac{17}{3}$��
��P������ΪP��$\frac{17}{3}$��$\frac{44}{9}$����
�������������������ĵ�P������Ϊ��11��36������$\frac{13}{3}$��$\frac{14}{9}$������$\frac{17}{3}$��$\frac{44}{9}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���������ֱ�������ε����ʡ�������Ǻ����Ķ��塢���������ε����ʺ��ж����������ҪӦ���˷������۵�˼�룬�������������ε����ʺͶ��κ����Ĺ�ϵʽ���г�����x�ķ����ǽ���Ĺؼ���


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
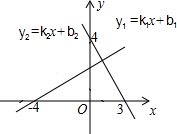 ��ͼ��ֱ��y1=k1x+b1�������ύ�ڵ㣨-4��0���ͣ�0��2.9����ֱ��y2=k2x+b2�������ύ�ڵ㣨3��0���ͣ�0��4��������ʽ��$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}��0}\\{{k}_{2}x+{b}_{2}��0}\end{array}\right.$�Ľ⼯�ǣ�������
��ͼ��ֱ��y1=k1x+b1�������ύ�ڵ㣨-4��0���ͣ�0��2.9����ֱ��y2=k2x+b2�������ύ�ڵ㣨3��0���ͣ�0��4��������ʽ��$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}��0}\\{{k}_{2}x+{b}_{2}��0}\end{array}\right.$�Ľ⼯�ǣ�������| A�� | x��-4 | B�� | x��3 | C�� | -4��x��3 | D�� | x��-4��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ȵĽ��ǶԶ��� | |
| B�� | ͬ���ڽ���ȣ���ֱ��ƽ�� | |
| C�� | ֱ����һ�㵽����ֱ�ߵĴ��߶Σ������㵽ֱ�ߵľ��� | |
| D�� | ����ֱ����һ�㣬����ֻ��һ��ֱ��������ֱ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����ͼ��ʽ�۵�һ�ŶԱ���ƽ�е�ֽ����EF���ۺۣ�����EFB=32�㣬��
����ͼ��ʽ�۵�һ�ŶԱ���ƽ�е�ֽ����EF���ۺۣ�����EFB=32�㣬��| A�� | �٢� | B�� | �ڢ� | C�� | �٢ۢ� | D�� | �ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ҹ��������趫������ʶ������ͼ��ʾ�����巶ΧΪ�������������캣��֮�������A��B��C������������������
�ҹ��������趫������ʶ������ͼ��ʾ�����巶ΧΪ�������������캣��֮�������A��B��C������������������| A | B | C | |
| ��γ���ȣ� | 31��00�� | 33��11�� | 25��38�� |
| �������ȣ� | 128��20�� | 125��00�� | 125��00�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com