

���� ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�C�����꣬���ݶԳƵ㣬�ɵ�D�����꣬���ݴ���ϵ�������ɵ�BD�Ľ���ʽ������ƽ���ߵĶԱ���ȣ��ɵù���m�ķ��̣����ݽⷽ�̣��ɵ�m��ֵ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��3�����ݻ��ഹֱ����ֱ�ߵı���ϵ����Ϊ���������ɵ�BD�Ĵ��ߣ����ݽⷽ���飬�ɵ�M�����꣮
��� �⣺��1����A��-1��0����B��4��0������y=ax2+bx+2����
$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$��
���κ�������ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����ͼ1��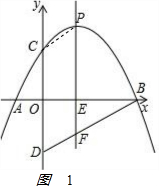 ��
��
��x=0ʱ��y=2��C������Ϊ��0��2����
�ɵ�D�ǵ�C����ԭ��ĶԳƵ㣬��D������Ϊ��0��-2����
��B��4��0����D��0��-2���ɵ�ֱ��BD�Ľ���ʽy=$\frac{1}{2}$x-2��
��E��������m��0������
F��m��$\frac{1}{2}$m-2����P��m��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2����
��PF=CD=4ʱ����-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��-��$\frac{1}{2}$m-2��=4��
���m=2��m=0����ȥ����
���E��������2��0����
��3����ͼ2��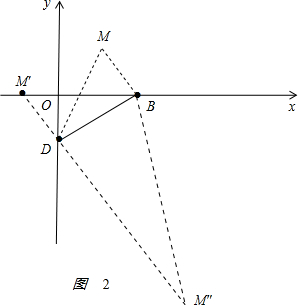 ��
��
��B��4��0����D��0��-2���ɵ�ֱ��BD�Ľ���ʽy=$\frac{1}{2}$x-2����
BM�Ľ���ʽΪy=-2x+8��
����BM�������ߣ���
$\left\{\begin{array}{l}{y=-2x+8}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$��$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$�����������⣬�ᣩ����M��3��2����
B��4��0����D��0��-2���ɵ�ֱ��BD�Ľ���ʽy=$\frac{1}{2}$x-2����
DM�Ľ���ʽΪy=-2x-2��
����DM�������ߣ���
$\left\{\begin{array}{l}{y=-2x-2}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=-18}\end{array}\right.$����M��-1��0����8��18����
������������M��������3��2������-1��0����8��-18����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ������ƽ���ı��εĶԱ���ȵó�����m�ķ����ǽ���ؼ������û��ഹֱ����ֱ�ߵı���ϵ����Ϊ�������ó�BD�Ĵ����ǽ���ؼ���


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
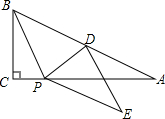 ��Rt��ABC�У���DΪб��AB���е㣬PΪAC��һ���㣬��BDP����PD���ڵ�ֱ�߶��ۣ���B�Ķ�Ӧ��ΪE��
��Rt��ABC�У���DΪб��AB���е㣬PΪAC��һ���㣬��BDP����PD���ڵ�ֱ�߶��ۣ���B�Ķ�Ӧ��ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����龳��
�����龳���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3������� | B�� | 4������� | C�� | 5������� | D�� | 7������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����B��4��1����
��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����B��4��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com