
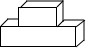
 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )| A. |  | B. | 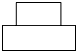 | C. |  | D. |  |
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.36×102 | B. | 0.36×103 | C. | 3.6×102 | D. | 3.6×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
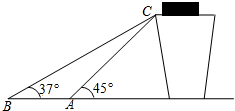 某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)
某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
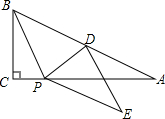 在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.
在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
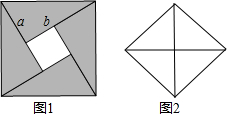 问题情境:
问题情境:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com