
| A. | 67.7×1012 | B. | 6.77×1013 | C. | 0.677×1014 | D. | 6.77×1014 |
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
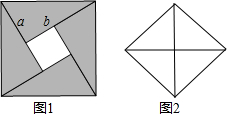 问题情境:
问题情境:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个单位长度 | B. | 4个单位长度 | C. | 5个单位长度 | D. | 7个单位长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
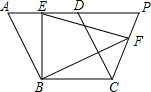 如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.
如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com