
【题目】如图,OA⊥OC,OB⊥OD,四位同学观察图形后分别说了自己的观点.
甲:∠AOB=∠COD;
乙:∠BOC+∠AOD=180°;
丙:∠AOB+∠COD=90°;
丁:图中小于平角的角有6个.
其中观点正确的有( )
A.甲、乙、丙
B.甲、丙、丁
C.乙、丙、丁
D.甲、乙、丁
【答案】D
【解析】解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°.
∴∠AOC﹣∠BOC=∠BOD﹣∠BOC.
∴∠AOB=∠COD.
∴甲同学说的正确;
∵∠BOC+∠AOD
=∠AOC+∠COD+∠BOC
=∠AOC+∠BOD
=90°+90°
=180°,
∴乙同学说的正确;
∵∠AOB+∠BOC=∠AOB=90°,∠BOC和∠COD不一定相等,
∴丙同学说的错误;
∵图中小于平角的角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD,共6个,
∴丁同学说的正确.
故选:D.
【考点精析】掌握余角和补角的特征是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关.


科目:初中数学 来源: 题型:
【题目】已知一张桌子配4张椅子,现有90立方米木料,若1立方米木料可做5张椅子或1张桌子,要使桌子和椅子刚好配套,设应该用x立方米的木料做桌子,则依题意可列方程为
A. 4x=5(90x) B. 5x=4(90x) C. x=4(90x)×5 D. 4x×5=90x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
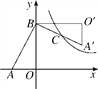
A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
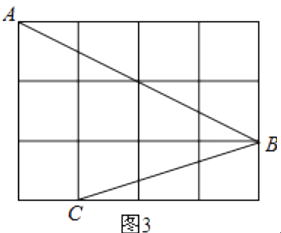
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点. 
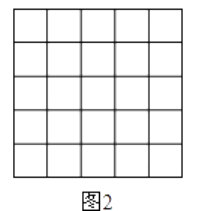
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 ![]() 、
、 ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
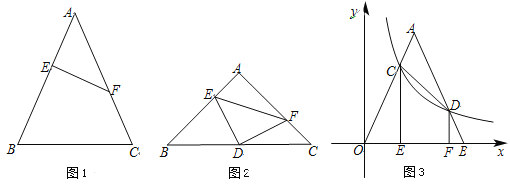
【题目】定义:如图1,等腰△ABC中,点E,F分别在腰AB,AC上,连结EF,若AE=CF,则称EF为该等腰三角形的逆等线.
(1)如图1,EF是等腰△ABC的逆等线,若EF⊥AB,AB=AC=5,AE =2,求逆等线EF的长;
(2)如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E,F分别在AB,AC上,求证:EF为等腰△ABC的逆等线;
(3)如图3,等腰△AOB的顶点O与原点重合,底边OB在x轴上,反比例函数y= ![]() (x>0)的图象交△OAB于点C,D,若CD恰为△AOB的逆等线,过点C,D分别作CE⊥x轴,DF⊥x轴,已知OE=2,求OF的长.
(x>0)的图象交△OAB于点C,D,若CD恰为△AOB的逆等线,过点C,D分别作CE⊥x轴,DF⊥x轴,已知OE=2,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间1小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com