
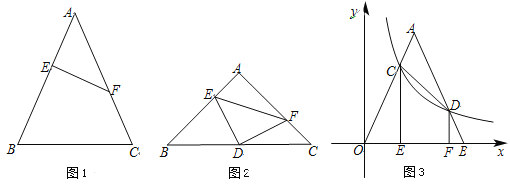
����Ŀ�����壺��ͼ1��������ABC�У���E��F�ֱ�����AB��AC�ϣ�����EF����AE��CF�����EFΪ�õ��������ε�����ߣ�
��1����ͼ1��EF�ǵ�����ABC������ߣ���EF��AB��AB��AC��5��AE ��2���������EF�ij���
��2����ͼ2��������ֱ����DEF��ֱ�Ƕ���Dǡ��Ϊ����ֱ����ABC�ױ�BC�ϵ��е㣬�ҵ�E��F�ֱ���AB��AC�ϣ���֤��EFΪ������ABC������ߣ�
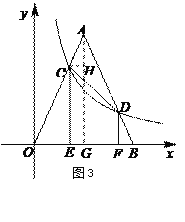
��3����ͼ3��������AOB�Ķ���O��ԭ���غϣ��ױ�OB��x���ϣ�����������y�� ![]() ��x��0����ͼ����OAB�ڵ�C��D����CDǡΪ��AOB������ߣ�����C��D�ֱ���CE��x�ᣬDF��x�ᣬ��֪OE��2����OF�ij���
��x��0����ͼ����OAB�ڵ�C��D����CDǡΪ��AOB������ߣ�����C��D�ֱ���CE��x�ᣬDF��x�ᣬ��֪OE��2����OF�ij���
���𰸡���1�������EF�ij�Ϊ![]() ��
��
��2��EF������ABC���������
��3��OF��2![]() ��2
��2
�����������������(1)����������ߵĶ���ó�CF=AE=2��AF=3�����ݹ��ɶ����ó�EF�ij��ȣ�(2)������AD����������֤������EDA�͡�FDCȫ�ȣ��Ӷ��ó�AE=CF���õ�����ߣ�(3)����OF=x����AG��OB��CH��AG����������ߵ����ʵó���ACH�͡�DBFȫ�ȣ��Ӷ��ó�EG=x-4�����ݡ�ACH�͡�COE���Ƶó�x��ֵ���Ӷ��ó�x��ֵ����OF�ij���.
�����������1����EF�ǵ�����ABC�������
��CF ��AE��2����AB��AC��5 ��AF��3 ��EF��AB ��EF��![]() ��
��![]()
��2������AD���ڵ���Rt��ABC�У���DΪ�ױ����е� ��AD��CD�ҡ�ADC��90��
�֡�DE��DF�ҡ�EDF��90�� ���EDA��90�㣭��ADF����FDC
���EDA�ա�FDC ��AE��CF ��EFΪ������ABC�������
��3����ͼ3����OF��x����DF��![]() ��AG��OB��CH��AG
��AG��OB��CH��AG
��CDΪ��AOB������� ��AC��BD���֡�ACH����AOB����DBF
�ҡ�AHC����AGO����DFB ���ACH�ա�DBF ��EG��CH��BF��AH��DF
��AO��AB����AG��OB ��OG��BG ��GF��BG��BF��OG��EG��OE
����EG��x��2��2��x��4 �ߡ�ACH�ס�COE ��![]() ��
��![]() ��
��![]() ��
��![]()
�����x2��4x��4��0 ����x��2![]() ��2 ��OF��2
��2 ��OF��2![]() ��2
��2



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѡ�ABCֽƬ��DE�۵�������A�����ı���BCDE�ڲ�ʱ�����A���1+��2֮����һ��������ϵʼ�ձ��ֲ��䣬��������һ��������ɣ���������ǣ� ��
A.��A=��1+��2
B.2��A=��1+��2
C.3��A=2��1+��2
D.3��A=2����1+��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OC��OB��OD����λͬѧ�۲�ͼ�κ�ֱ�˵���Լ��Ĺ۵㣮
�ף���AOB=��COD��
�ң���BOC+��AOD=180�㣻
������AOB+��COD=90�㣻
����ͼ��С��ƽ�ǵĽ���6����
���й۵���ȷ���У� ��
A.�ס��ҡ���
B.�ס�������
C.�ҡ�������
D.�ס��ҡ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a2a3=a6
B.����a3��2=��a6
C.����3a2��2=6a4
D.����a+b����a+b��=b2��a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A. 3a2+a2=4a4 B. (a2)3=a5 C. a��a2=a3 D. (2a)3=6a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��b���������������������ϵĶ�Ӧ���λ����ͼ��ʾ����a����a��b����b���մ�С�����˳�����У� �� ![]()
A.��b����a��a��b
B.a����b��b����a
C.��b��a����a��b
D.a����b����a��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���һ�����е������ǣ�������
A. �ı߶����B. �Խ����C. �Խ������D. ����Գ�ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AD=5��AB=7����EΪDC��һ�����㣬�ѡ�ADE��AE�۵�������D�Ķ�Ӧ��D�����ڡ�ABC�Ľ�ƽ������ʱ��DE�ij�Ϊ �� 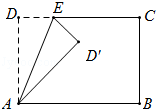
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com