
����Ŀ����ͼ��������y=��x2��2x+3��ͼ����x�ύA��B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣮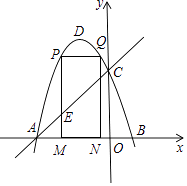
��1�����A��B��C�����ꣻ
��2����MΪ�߶�AB��һ�㣨��M�����A��B�غϣ�����M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P����P��PQ��AB���������ڵ�Q����Q��QN��x����N��������PMNQ���ܳ����ʱ�����AEM�������
��3���ڣ�2���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG=2 ![]() DQ�����F�����꣮
DQ�����F�����꣮
���𰸡�
��1��
�⣺��y=0ʱ����x2��2x+3=0�����x1=1��x2=��3����A����3��0����B��1��0������x=0ʱ��y=��x2��2x+3=3����C��0��3����
��2��
�⣺�����ߵĶԳ���Ϊֱ��x=��1��
��M��x��0�������P��x����x2��2x+3��������3��x����1����
�ߵ�P���Q����ֱ��=��1�Գƣ�
���Q����2��x����x2��2x+3����
��PQ=��2��x��x=��2��2x��
�����PMNQ���ܳ�=2����2��2x��x2��2x+3��=��2x2��8x+2=��2��x+2��2+10��
��x=��2ʱ������PMNQ���ܳ����ʱM����2��0����
��ֱ��AC�Ľ���ʽΪy=kx+b��
��A����3��0����C��0��3������� ![]() �����
����� ![]() ��
��
��ֱ��AC�Ľ���ʽΪy=3x+3��
��x=��2ʱ��y=x+3=1��
��E����2��1����
���AEM�����= ![]() ������2+3����1=
������2+3����1= ![]() ��
��
��3��
�⣺��x=��2ʱ��Q��0��3��������C���Q�غϣ�
��x=��1ʱ��y=��x2��2x+3=4����D����1��4����
��DQ= ![]() =
= ![]() ��
��
��FG=2 ![]() DQ=2
DQ=2 ![]() ��
�� ![]() =4��
=4��
��F��t����t2��2t+3������G��t��t+3����
��GF=t+3������t2��2t+3��=t2+3t��
��t2+3t=4�����t1=��4��t2=1��
��F����������4����5����1��0����
����������1���ⷽ�̩�x2��2x+3=0�ɵ�A���B�����ꣻ�����Ա���Ϊ0ʱ�ĺ���ֵ�ɵõ�C�����ꣻ��2����ȷ�������ߵĶԳ���Ϊֱ��x=��1����M��x��0�������P��x����x2��2x+3��������3��x����1�������öԳ��Եõ���Q����2��x����x2��2x+3����PQ=��2��2x�����Ծ���PMNQ���ܳ�=2����2��2x��x2��2x+3�������ö��κ����õ���x=��2ʱ������PMNQ���ܳ����ʱM����2��0�����������ô���ϵ����ȷ��ֱ��AC�Ľ���ʽΪy=3x+3���Ӷ��õ�E����2��1����Ȼ����������������ʽ��⣻��3����x=��2ʱ�õ�Q��0��3������ȷ��D����1��4������DQ= ![]() ������FG=2
������FG=2 ![]() DQ=4����F��t����t2��2t+3������G��t��t+3��������GF=t+3������t2��2t+3��=t2+3t�����ǵõ�����t2+3t=4��Ȼ��ⷽ�����t���ɵõ�F�����꣮
DQ=4����F��t����t2��2t+3������G��t��t+3��������GF=t+3������t2��2t+3��=t2+3t�����ǵõ�����t2+3t=4��Ȼ��ⷽ�����t���ɵõ�F�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��AB��CD�ཻ�ڵ�O����֪OEƽ����BOD������AOC����AOD=3��7��

��1������DOE�Ķ�����
��2����OF��OE������COF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
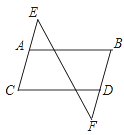
����Ŀ����ͼ��������3�仰����AB��CD���ڡ�B=��C���ۡ�E=��F����������2�仰Ϊ�����������仰Ϊ���۹�������.
��1���㹹������ļ������⣿
��2���㹹���������������Ǽ����⣿�����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
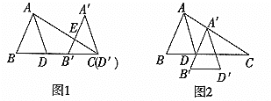
����Ŀ����ͼ1��ƽ��������ABD��ʹ��D��BD���ӳ���ƽ������C���õ���������A'B'D'��A'B'��AC�ڵ�E��ADƽ�֡�BAC��
��1��������B'EC���A'֮��Ĺ�ϵ����д�����ɣ�
��2�������������ABDƽ������ͼ2��ʾλ�ã��õ���A'B'D'��������A'D'ƽ�֡�B'A'C��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD��BC����A=90�㣬AD=1cm��AB=3cm��BC=5cm������P�ӵ�B������1cm/s���ٶ���BC�ķ����˶�������Q�ӵ�C������2cm/s���ٶ���CD�����˶���P��Q����ͬʱ��������Q�����Dʱֹͣ�˶�����PҲ��ֹ֮ͣ�����˶���ʱ��Ϊts��t��0�� 
��1�����߶�CD�ij���
��2��tΪ��ֵʱ���߶�PQ���ı���ABCD�������Ϊ1��2�����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC��D��BD=AD��DG=DC��E��F�ֱ���BG��AC���е㣮
��1����֤��DE=DF��DE��DF��
��2������EF����AC=10����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�ʽ��x��ֵ.
(1) (x-1)3=27;
(2)x3+1=-![]() ;
;
(3)![]() (2x+3)3=54;
(2x+3)3=54;
(4) 27(2x-1)3+2=66.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��A�ǡ�O��һ�㣬�뾶OC���ӳ��������A��ֱ�߽���B�㣬OC=BC��AC= ![]() OB��
OB�� 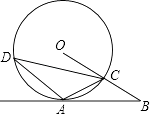
��1����֤��AB�ǡ�O�����ߣ�
��2������ACD=45�㣬OC=2������AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��ѧ��ȤС�龭���г����飬�õ�ij��ͼ��ÿ�µ��������ۼ۵Ĺ�ϵΪ������ϵ���±���
�ۼۣ�Ԫ/���� | 50 | 55 | 60 | 65 | �� |
������������ | 2000 | 1800 | 1600 | 1400 | �� |
��֪��ͼ��Ľ���Ϊÿ��30Ԫ�����ۼ�ΪxԪ��
��1�����ú�x��ʽ�ӱ�ʾ�������۸�ͼ��ÿ����������Ԫ��������������������x��ʾֱ��д�������
��2��������ͼ���������Ϊ48000Ԫ����ÿ��ͼ����Ҫ�ۼ۶���Ԫ��
��3�������۸�ͼ���������ΪyԪ����ô�ۼ�Ϊ����ʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com