
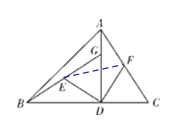
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由已知条件先证△BDG≌△ADC,再证△BDE≌△ADF即可得到所求结论;
(2)如图,由(1)可知∠ADC=90°,△DEF是等腰直角三角形, 结合F是AC的中点可得DF=![]() AC=5,这样用勾股定理即可求得EF的长度.
AC=5,这样用勾股定理即可求得EF的长度.
试题解析:
(1)∵AD⊥BC于点D,
∴∠BDG=∠ADC=90°.
∵BD=AD,DG=DC,
∴△BDG≌△ADC,
∴BG=AC.
∵E,F分别是BG,AC的中点,
∴DE=![]() BG,DF=
BG,DF=![]() AC.
AC.
∴DE=DF.
又∵BD=AD,BE=AF,
∴△BDE≌△ADF.
∴∠BDE=∠ADF.
∴∠EDF=∠EDG+∠ADF=∠EDG+∠BDE=∠BDG=90°.
∴DE⊥DF.
(2)如图,连接EF,
∵AC=10,∠ADC=90°,
∴DE=DF=![]() AC=5.
AC=5.
又∵∠EDF=90°,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( ) 
A.150°
B.210°
C.105°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明计划三天看完一本书,预计第一天看 x 页,第二天看的页数比第一天看的页数多50 页,第三天看的页数比第二天看的页数的一半还少5页.
(1)用含x的式子表示这本书的页数;
(2)若 x=100,则这本书共有多少页?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列四种结论:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是( )
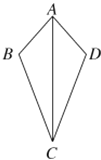
A. ①② B. ①③ C. ①④ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com