
����Ŀ����1��һ����λ��������a��ʾʮλ�ϵ����֣�b��ʾ��λ�ϵ����֣�a��b��ab��0�����������λ���ö���ʽ��ʾΪ�� ������a��b��ʽ�ӣ�������ʮλ����λ�ϵ����ֻ���λ�õõ�һ������λ��������������λ���ĺ�һ���ܱ��� ����������������λ���IJ�һ���ܱ��� ������
��2��һ����λ������F��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0���������İ�λ��ʮλ����λ�ϵ�����������ѡ�������������6����ͬ����λ��������6����λ���ĺ͵��������λ�������������������λ��FΪ���Ѻ����������磺132�����Ѻ�����
һ����λ������P��������λ�ϵ����ֻ�����ͬ�Ҷ���Ϊ0��������ʮλ���ֵ��ڰ�λ�������λ���ֵĺͣ������������λ��PΪ����ƽ����
��ֱ���ж�123�Dz������Ѻ�������
��ֱ��д�������� ��������ƽ����
��ͨ���з��̵ķ��������������ƽ�����������Ѻ�����������
���𰸡�(1) 10a+b��11��9��(2) ��123���ǡ��Ѻ����������ɼ���������32���ۼ��ǡ���ƽ�������ǡ��Ѻ�����������396��264��132��
��������
��1���ֱ���������ĺ��������IJ�ɵõ����ۣ�
��2���ٸ������Ѻ������Ķ����жϼ��ɣ�
�ڸ�������ƽ�����Ķ����оٳ����е�����ƽ�������ɣ�
������λ��![]() ��������ƽ�����������Ѻ���������������ƽ�����Ķ��壬�ó�y��x+z���������Ѻ������Ķ��壬�ó�10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z������Ϊ12y��78x��21z����y��x+z���룬�����ó�z��2x��Ȼ��Ӣڵ���������ѡ������Ҫ���������
��������ƽ�����������Ѻ���������������ƽ�����Ķ��壬�ó�y��x+z���������Ѻ������Ķ��壬�ó�10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z������Ϊ12y��78x��21z����y��x+z���룬�����ó�z��2x��Ȼ��Ӣڵ���������ѡ������Ҫ���������
(1)�����λ���ö���ʽ��ʾΪ10a+b��
��10a+b��+��10b+a����10a+b+10b+a��11a+11b��11��a+b����
��11��a+b����11��a+b����������
�������λ���ĺ�һ���ܱ���11������
��10a+b������10b+a����10a+b��10b��a��9a��9b��9��a��b����
��9��a��b����9��a��b����������
����������λ���IJ�һ���ܱ���9������
�ʴ�Ϊ��11��9��
(2)��123���ǡ��Ѻ��������������£�
��12+21+13+31+23+32��132��123��
��123���ǡ��Ѻ�������
��ʮλ������9�ġ���ƽ������198��297��396��495��594��693��792��891��һ��8����
ʮλ������8�ġ���ƽ������187��286��385��584��682��781��һ��6����
ʮλ������7�ġ���ƽ������176��275��374��473��572��671��һ��6����
ʮλ������6�ġ���ƽ������165��264��462��561��һ��4����
ʮλ������5�ġ���ƽ������154��253��352��451��һ��4����
ʮλ������4�ġ���ƽ������143��341��һ��2����
ʮλ������3�ġ���ƽ������132��231��һ��2����
���ԣ�����ƽ����һ����8+��6+4+2����2��32����
�ʴ�Ϊ32��
������λ��![]() ���ǡ���ƽ�������ǡ��Ѻ�������
���ǡ���ƽ�������ǡ��Ѻ�������
����λ��![]() �ǡ���ƽ������
�ǡ���ƽ������
��y��x+z��
��![]() �ǡ��Ѻ�������
�ǡ��Ѻ�������
��10x+y+10y+x+10x+z+10z+x+10y+z+10z+y��100x+10y+z��
��22x+22y+22z��100x+10y+z��
��12y��78x��21z��
��y��x+z���룬��12x+12z��78x��21z��
��33z��66x��
��z��2x��
������֪�����ǡ���ƽ�������ǡ��Ѻ�����������396��264��132��


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��1��1����B��4��3��������A����ƽ��2����λ���ȣ�������ƽ��3����λ���ȵõ���C��
��1��д����C�����ꣻ
��2��������ABC���жϡ�ABC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�У�AB=AC=10���ף�BC=12���ף�D��BC���е㣬��P��B��������a����/�루a��0�����ٶ���BA�������A�˶�����Qͬʱ��1����/����ٶȴ�D��������DB�������B�˶�������һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶����������˶���ʱ��Ϊt�룮 
��1����a=2����BPQ�ס�BDA����t��ֵ��
��2�����M��AC�ϣ��ı���PQCMΪƽ���ı��Σ� 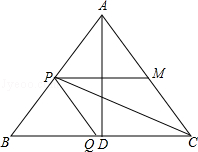
����a= ![]() ����PQ�ij���
����PQ�ij���
���Ƿ����ʵ��a��ʹ�õ�P�ڡ�ACB��ƽ�����ϣ������ڣ������a��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
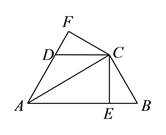
����Ŀ����ͼ������ABC�У�AD��BC��D��BD=AD��DG=DC��E��F�ֱ���BG��AC���е㣮
��1����֤��DE=DF��DE��DF��
��2������EF����AC=10����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��AB���е㣬��AC��12��BC��5��CD��6.5.��֤����ABC��ֱ�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ����![]() ����
����![]()
A. �������Ǻ�һ���߶�Ӧ��ȵ�����������ȫ��
B. ��һ���ߺ�һ����Ƕ�Ӧ��ȵ�����ֱ��������ȫ��
C. �����ߺ�����һ�ߵĶԽǶ�Ӧ��ȵ�����������ȫ��
D. ������ֱ�DZ߶�Ӧ��ȵ�����ֱ��������ȫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ƽ��
ƽ��![]() ��
�� ![]() ��
��![]() ��
�� ![]() ��
��![]() ����
����![]() ��
��
��![]() ����֤��
����֤�� ![]() ��
��![]() ��
��
��![]() ����
����![]() ��
�� ![]() ��
�� ![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��B��C��ͬһֱ���ϣ�M��N�ֱ���AB��BC���е㣮
(1)��AB=20��BC =8����MN�ij���
(2)��AB =a��BC =8����MN�ij���
(3)��AB =a��BC =b����MN�ij���
(4)��(1)(2)(3)�Ľ�����ܵõ�ʲô���ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
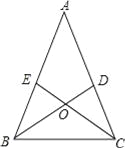
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABC����ACB��ƽ����BD��CE�ཻ��O�㣬��BD��AC�ڵ�D��CE��AB�ڵ�E��ijͬѧ����ͼ�κ�ó����½��ۣ���������һ����ȷ����______������ţ���
�١�BCD�ա�CBE���ڡ�BAD�ա�BCD���ۡ�BDA�ա�CEA���ܡ�BOE�ա�COD���ݡ�ACE�ա�BCE��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com