
【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒. 
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形. 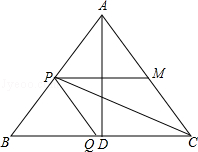
①若a= ![]() ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.
【答案】
(1)解:△ABC中,AB=AC=10cm,BC=12cm,D是BC的中点,
∴BD=CD= ![]() BC=6cm,
BC=6cm,
∵a=2,
∴BP=2tcm,DQ=tcm,
∴BQ=BD﹣QD=6﹣t(cm),
∵△BPQ∽△BDA,
∴ ![]() ,
,
即 ![]() ,
,
解得:t= ![]()
(2)解:①过点P作PE⊥BC于E,
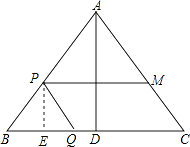
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,
∴PB=CM,
∴PB=PQ,
∴BE= ![]() BQ=
BQ= ![]() (6﹣t)cm,
(6﹣t)cm,
∵a= ![]() ,
,
∴PB= ![]() tcm,
tcm,
∵AD⊥BC,
∴PE∥AD,
∴PB:AB=BE:BD,
即 ![]() ,
,
解得:t= ![]() ,
,
∴PQ=PB= ![]() t=
t= ![]() (cm);
(cm);
②不存在.理由如下:
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,∴PB=CM,∴PB=PQ.
若点P在∠ACB的平分线上,则∠PCQ=∠PCM,
∵PM∥CQ,
∴∠PCQ=∠CPM,
∴∠CPM=∠PCM,
∴PM=CM,
∴四边形PQCM是菱形,
∴PQ=CQ,PM∥CQ,
∴PB=CQ,PM:BC=AP:AB,
∵PB=atcm,CQ=CD+QD=6+t(cm),
∴PM=CQ=6+t(cm),AP=AB﹣PB=10﹣at(cm),
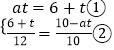 ,
,
化简得②:6at+5t=30③,
把①代入③得,t=﹣ ![]() ,
,
∴不存在实数a,使得点P在∠ACB的平分线上
【解析】(1)由△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,根据等腰三角形三线合一的性质,即可求得BD与CD的长,又由a=2,△BPQ∽△BDA,利用相似三角形的对应边成比例,即可求得t的值;(2)①首先过点P作PE⊥BC于E,由四边形PQCM为平行四边形,易证得PB=PQ,又由平行线分线段成比例定理,即可得方程 ![]() ,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.
,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图所示,某地有一地下工程,其底面是正方形,面积为405m2,四个角是面积为5m2的小正方形渗水坑,根据这些条件如何求a的值?与你的同伴进行交流.
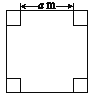
下面是小康提供的解题方案,根据解题方案请你完成本题的解答过程:
①设大正方形的边长为x m,小正方形的边长为y m,那么根据题意可列出关于x的方程为_______,关于y的方程为_______;
②利用平方根的意义,可求得x=________(取正值,结果保留根号),y=________(取正值,结果保留根号);
③所以a=x-2y=____________=__________(结果保留根号);
④答:________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( ) 
A.150°
B.210°
C.105°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明计划三天看完一本书,预计第一天看 x 页,第二天看的页数比第一天看的页数多50 页,第三天看的页数比第二天看的页数的一半还少5页.
(1)用含x的式子表示这本书的页数;
(2)若 x=100,则这本书共有多少页?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 
(1)求证:CF与⊙O相切;
(2)若DEDC=13,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com