
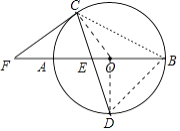
【题目】如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 
(1)求证:CF与⊙O相切;
(2)若DEDC=13,求⊙O的半径.
【答案】
(1)解:连接OC、OD.
∵ ![]() =
= ![]() ,
,
∴OD⊥AB,∠AOD=90°,
∵FE=FC,
∴∠FCE=∠FEC,
∵OC=OD,
∴∠OCE=∠ODC,
∴∠FCO=∠FCE+∠OCE=∠FEC+∠EDO=∠OED+∠ODC=90°.
∴OC⊥CF,
∴CF是⊙⊙O的切线
(2)解:连接BC、BD.

∵ ![]() =
= ![]() ,
,
∠EBD=∠BCD,
∵∠BDE=∠CDB,
∴△BDE∽△CDB,
∴ ![]() =
= ![]() ,
,
∴BD2=CDED=13,
∵∠BOD=90°,
∴OB2+OD2=BD2=13,
∴OB2= ![]() ,
,
∴OB= ![]() ,
,
∴⊙O的半径为 ![]()
【解析】(1)欲证明CF与⊙O相切,只要证明OC⊥CF即可.(2)由△BDE∽△CDB,推出 ![]() =
= ![]() ,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB=
,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB= ![]() 解决问题.
解决问题.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒. 
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形. 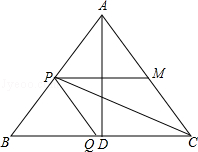
①若a= ![]() ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C在同一直线上,M、N分别是AB,BC的中点.
(1)若AB=20,BC =8,求MN的长;
(2)若AB =a,BC =8,求MN的长;
(3)若AB =a,BC =b,求MN的长;
(4)从(1)(2)(3)的结果中能得到什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校甲、乙两班分别有一男生和一女生共4名学生报名竞选校园广播播音员.
(1)若从甲、乙两班报名的学生中分别随机选1名学生,则所选的2名学生性别相同的概率是多少?
(2)若从报名的4名学生中随机选2名,求这2名学生来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间小王和小吴两家6个人一起外出旅游,乘坐两辆出租车前往飞机场,在离机场11千米处一辆车出了故障,不能行驶.此时离机场停止办理登机手续时间还有半个小时,唯一可以利用的交通工具只有一辆出租车,连同司机在内限乘5人,车速60千米/时.
(1)如果2人在原地等候,这辆车分两批接送,6人都能及时到达机场吗?
(2)如果在汽车送第一批人的同时,余下2人以6千米/时的速度向前步行,汽车在将第一批人送达后即返回接第二批人,他们能及时到达机场吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
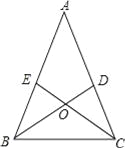
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产了台数相同A型、B型两种单价不同的计算机,B型机的单价比A型机的便宜0.24万元,已知A型机总价值120万元,B型计算机总价值为80万元,求A型、B型两种计算机的单价,设A型计算机的单价是x万元,可列方程_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com