
【题目】如图,已知![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]() .
.
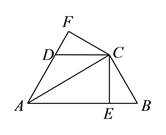
【解析】试题分析:(1)已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,根据角平分线的性质定理可得CE=CF,再由![]() ,根据HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL证明Rt△AFC≌△Rt△AEC,即可得AE=AF,设DF=x,则有9+x=21-x,得x=6,在Rt△CDF中,根据勾股定理求得CF=8,在Rt△AFC中,再运用勾股定理求得AC即可.
,根据HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL证明Rt△AFC≌△Rt△AEC,即可得AE=AF,设DF=x,则有9+x=21-x,得x=6,在Rt△CDF中,根据勾股定理求得CF=8,在Rt△AFC中,再运用勾股定理求得AC即可.
试题解析:
(![]() )证明:∵
)证明:∵![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() .
.
(![]() )由(
)由(![]() )得,
)得, ![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
设![]() ,则有
,则有![]() ,得
,得![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
①当a=5时,方程组的解是![]() ;
;
②当x,y的值互为相反数时,a=20;
③不存在一个实数a使得x=y;
④若![]() ,则a=2.
,则a=2.
A. ①②④ B. ②③④ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
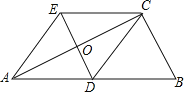
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,直线AB,CD相交于点O,点P为射线OC上异于O的一个点.
(1)请用你手中的数学工具画出∠AOC的平分线OE;
(2)过点P画出(1)中所得射线OE的垂线PM(垂足为点M),并交直线AB于点N;
(3)请直接写出上述所得图形中的一对相等线段 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板, ![]() ,
, ![]() .
.
(![]() )要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图
)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图![]() ),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(![]() )图
)图![]() 中甲种剪法称为第
中甲种剪法称为第![]() 次剪取,记所得正方形面积为
次剪取,记所得正方形面积为![]() ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为![]() (如图
(如图![]() ),则
),则![]() __________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第
__________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第![]() 次剪取,并记这四个正方形面积和为
次剪取,并记这四个正方形面积和为![]() ,继续操作下去,则第
,继续操作下去,则第![]() 次剪取时,
次剪取时, ![]() __________.
__________.
(![]() )求第
)求第![]() 次剪取后,余下的所有小三角形的面积之和__________.
次剪取后,余下的所有小三角形的面积之和__________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A![]() 、B
、B![]() 、C
、C![]() .将其平移后得到
.将其平移后得到![]() ,若A,B的对应点是
,若A,B的对应点是![]() ,
,![]() ,C的对应点
,C的对应点![]() 的坐标是
的坐标是![]() .
.
(1)在平面直角坐标系中画出△ABC;
(2)写出点![]() 的坐标是_____________,
的坐标是_____________,![]() 坐标是___________;
坐标是___________;
(3)此次平移也可看作![]() 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形ABCD和边长为b(a>b)的正方形CEFG拼在一起,B、C、E三点在同一直线上,设图中阴影部分的面积为S.



图① 图② 图③
(1)如图①,S的值与a的大小有关吗?说明理由;
(2)如图②,若a+b=10,ab=21,求S的值;
(3)如图③,若a-b=2,![]() =7,求
=7,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com