
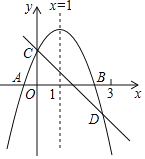
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论错误的是( )
A.2a+b+c>0
B.a<﹣1
C.x(ax+b)≤a+b
D.双曲线y=![]() 的两分支分别位于第一、第三象限
的两分支分别位于第一、第三象限
【答案】D
【解析】
A、根据抛物线与y轴的交点在x轴上方可得c>0,由抛物线的对称轴为直线x=1可得b=﹣2a,进而可判断2a+b+c的符号;
B、根据图象可知当x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,再把b=﹣2a代入即可判断;
C、根据图象可知当x=1时,二次函数有最大值,即ax2+bx+c≤a+b+c,从而可得ax2+bx≤a+b;
D、根据题意并结合二次函数的对称性可知抛物线与x轴的另一个交点在点(﹣1,0)右侧,从而得当x=﹣1时,y<0,即a﹣b+c<0,再根据反比例函数的性质即可判断.
解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以A正确,不符合题意;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,
所以B正确,不符合题意;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,
所以C正确,不符合题意;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
∴双曲线y=![]() 的两分支分别位于第二、第四象限
的两分支分别位于第二、第四象限
所以D错误,符合题意,
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明骑电动车从甲地去乙地,而小刚骑自行车从乙地去甲地,两人同时出发走相同的路线;设小刚行驶的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系,点B的坐标为(![]() ,0). 根据图象进行探究:
,0). 根据图象进行探究:

(1)两地之间的距离为 km;
(2)请解释图中点B的实际意义;
(3)求两人的速度分别是每分钟多少km?
(4)求线段BC所表示的y与x之间的函数关系式;并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
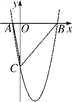
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C,连接AC,BC.
(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
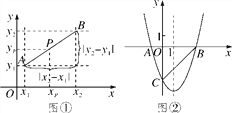
【题目】阅读材料:如图①,在平面直角坐标系中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),AB的中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=![]() ,同理得yp=
,同理得yp=![]() ,所以AB的中点坐标为P(
,所以AB的中点坐标为P(![]() ,
,![]() ).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=
).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=![]() .
.
注:上述公式对A,B在平面直角坐标系中其他位置也成立.
解答下列问题:
如图②,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,与y轴交于点C,且BO=OC=3AO,连接BC.
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,试求出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的文字,然后按要求解题:
例:1+2+3+ … +100=?
如果一个一个顺次相加显然太繁琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法运算律,是可以大大简化计算,提高运算速度的.
因为1+100=2+99=3+98= … =50+51=101
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+ … +100
=(1+100)+(2+99)+(3+98)+ … +(50+51)
=101×____________
=____________ .
(1)补全例题的解题过程;
(2)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)

(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() .
.

(1)试说明![]() 成立的理由.(完成下面的填空)
成立的理由.(完成下面的填空)
证明:![]() ,
,
![]() ,(________________)
,(________________)
又![]() ,(已知)
,(已知)
![]() ,(________________)
,(________________)
![]() .(________________)
.(________________)
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com