
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.

(1)求证:△AEB≌△CDA;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求BE的长.
【答案】(1)见解析;(2)60°;(3)14
【解析】
(1)根据等边三角形的性质,通过全等三角形的判定定理SAS证得结论;
(2)利用(1)中的全等三角形的对应角相等和三角形外角的性质,即可求得∠BPQ=60°;
(3)利用(2)的结果求得∠PBQ=30°,所以由“30度角所对的直角边是斜边的一半”得到2PQ=BP=12,则易求BE=BP+PE=14.
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中,
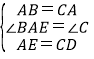 ,
,
∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP,
即∠BPQ=∠BAC=60°;
(3)∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=30°,
∴BP=2PQ=12,
∴BE=BP+PE=12+2=14


科目:初中数学 来源: 题型:
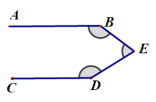
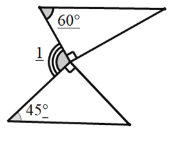
【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
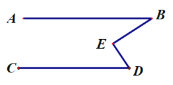
证明如下:过E点作EF∥AB.
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
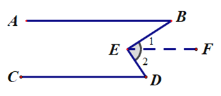
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
[创新应用]:
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )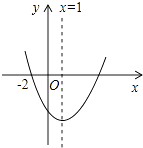
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定:出租车起步价允许行驶的最远路程为3km,超过3km的部分每千米另收费,甲说:“我乘这种出租车走了9km,付了14元.”乙说:“我乘这种出租车走了13千米,付了20元”.请你算出这种出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
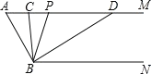
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
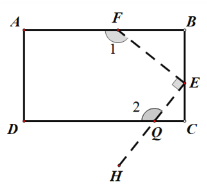
【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.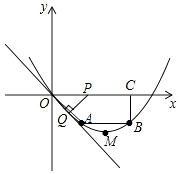
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )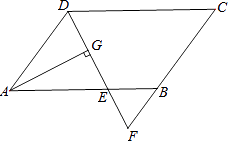
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
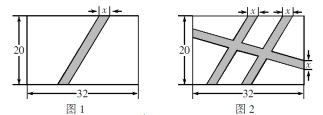
【题目】学校课外生物小组的试验园地是长32m、宽20m的矩形,为便于管理,现要在试验园地开辟水平宽度均为xm的小道(图中阴影部分).
(1)如图1,在试验园地开辟一条水平宽度相等的小道,则剩余部分面积为 m2(用含x的代数式表示);
(2)如图2,在试验园地开辟水平宽度相等的三条小道,其中有两条道路相互平行. 若使剩余部分面积为570m2,试求小道的水平宽度x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com