Question

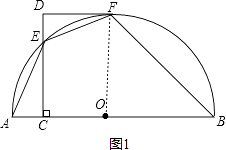
【题目】如图，AB是半圆O的直径，CD⊥AB于点C，交半圆于点E，DF切半圆于点F．已知∠AEF=135°．
（1）求证：DF∥AB；
（2）若OC=CE，BF= ，求DE的长．

Answer 1

【答案】
（1）证明：连接OF，

∵A、E、F、B四点共圆，

∴∠AEF+∠B=180°，

∵∠AEF=135°，

∴∠B=45°，

∴∠AOF=2∠B=90°，

∵DF切⊙O于F，

∴∠DFO=90°，

∵DC⊥AB，

∴∠DCO=90°，

即∠DCO=∠FOC=∠DFO=90°，

∴四边形DCOF是矩形，

∴DF∥AB

（2）解：过E作EM⊥BF于M，

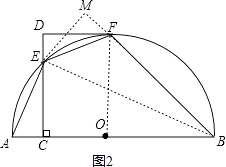
∵四边形DCOF是矩形，

∴OF=DC=OA，

∵OC=CE，

∴AC=DE，

设DE=x，则AC=x，

∵在Rt△FOB中，∠FOB=90°，OF=OB，BF=2 ，由勾股定理得：OF=OB=2，

则AB=4，BC=4﹣x，

∵AC=DE，OCDF=CE，

∴由勾股定理得：AE=EF，

∴∠ABE=∠FBE，

∵EC⊥AB，EM⊥BF

∴EC=EM，∠ECB=∠M=90°，

在Rt△ECA和Rt△EMF中

∴Rt△ECA≌Rt△EMF，

∴AC=MF=DE=x，

在Rt△ECB和Rt△EMB中，由勾股定理得：BC=BM，

∴BF=BM﹣MF=BC﹣MF=4﹣x﹣x=2 ，

解得：x=2﹣ ，

即DE=2﹣ ．

【解析】（1）证明：连接OF，根据圆内接四边形的性质得到∠AEF+∠B=180°，由于∠AEF=135°，得出∠B=45°，于是得到∠AOF=2∠B=90°，由DF切⊙O于F，得到∠DFO=90°，由于DC⊥AB，得到∠DCO=90°，于是结论可得；（2）过E作EM⊥BF于M，由四边形DCOF是矩形，得到OF=DC=OA，由于OC=CE，推出AC=DE，设DE=x，则AC=x，在Rt△FOB中，∠FOB=90°，OF=OB，BF=2 ，由勾股定理得：OF=OB=2，则AB=4，BC=4﹣x，由于AC=DE，OCDF=CE，由勾股定理得：AE=EF，通过Rt△ECA≌Rt△EMF，得出AC=MF=DE=x，在Rt△ECB和Rt△EMB中，由勾股定理得：BC=BM，问题可得．
【考点精析】通过灵活运用切线的性质定理，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题．