七年级学生参加了社会实践调查活动,到生态果园调查后得到如下信息:今年收获了15吨李子和8吨桃子,要租用甲、乙两种货车共6辆,及时运往外地,经询问,甲种货车可装李子4吨和桃子1吨,乙种货车可装李子1吨和桃子3吨.根据同学们带回的信息,试探究以下问题:
(1)共有几种租车方案?
(2)经咨询运输公司,甲种货车每辆需付运费1000元,乙种货车每辆需付运费700元,试帮助选出最佳方案,并求出此方案运费是多少.
请同学们补充完成下列部分解题过程:
(1)解:
①若设租用甲车x辆,则租用乙车______辆,
②由题意可知:甲车一共可装______吨桃子,乙车一共可装______吨桃子,则甲,乙两种车一共可装______吨桃子.(用含有x的代数式表示)
请列出不等式______
③甲车一共可装______吨李子,乙车一共可装______吨李子,则甲,乙两种车一共可装______吨李子.(用含有x的代数式表示)
请列出不等式______
④请列出不等式组,并求出满足不等组的整数解,写出相应的方案
(2)解:
解:(1)①若设租用甲车x辆,则租用乙车 (6-x)辆,
②由题意可知:甲车一共可装 x吨桃子,乙车一共可装 3(6-x)吨桃子,则甲,乙两种车一共可装 x+3(6-x)吨桃子.(用含有x的代数式表示)
请列出不等式 x+3(6-x)≥8,
③甲车一共可装 4x吨李子,乙车一共可装 (6-x)吨李子,则甲,乙两种车一共可装 4x+(6-x)吨李子.(用含有x的代数式表示)
列出不等式 4x+(6-x)≥15,
④
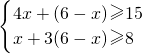
3≤x≤5.
当甲为3辆时,乙为3辆.
当甲为4辆时,乙为2辆.
当甲为5辆时,乙为1辆.
所以有3种方案.
(2)当甲为3辆,乙为3辆时最省钱.
1000×3+700×3=5100(元).
最省钱的运费是5100元.
分析:(1)设甲种货车为x辆,乙种货车为(6-x)辆,根据生态果园今年收获了15吨李子和8吨桃子,要租用甲、乙两种货车共6辆,及时运往外地,甲种货车最多可同时装4吨李子和1吨桃子,乙种最多可同时装1吨李子和3吨桃子可列出不等式组求解.
(2)根据甲种货车每辆需运费1000元,乙种货车每辆需运费700元,可知道甲越少越省钱.
点评:本题考查一元一次不等式组的应用,关键是以收获的李子和桃子数做为不等量关系列不等式组求解,以及根据甲车最少时,最省钱从而可求出方案.

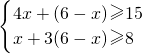


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案