
 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=| 3 |
 |
| BC |
 |
| BD |
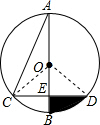 解:连接OC,OD,
解:连接OC,OD,| 3 |
 |
| BC |
 |
| BD |
| CE |
| AC |
| 1 |
| 2 |
| CE |
| OC |
| 1 |
| OC |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
60π×(
| ||||
| 360 |
| 1 |
| 2 |
| ||
| 3 |
| 2π |
| 9 |
| ||
| 6 |
| 2π |
| 9 |
| ||
| 6 |


科目:初中数学 来源: 题型:
| A、950×1010km |
| B、95×1012km |
| C、9.5×1012km |
| D、0.95×1013km |
查看答案和解析>>
科目:初中数学 来源: 题型:
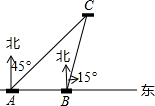 马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号)
马航失联客机MH370引起全球高度关注,为了搜寻客机残骸,我国派出多艘军舰和海监船到达失事海域进行搜寻,如图,前往南印度洋某海域的我井冈山舰A和昆仑山舰B自西向东航行,B舰在A舰的正东方向,且亮剑保持20海里的距离,某一时刻两舰同时测得在A的东北方向,B的北偏东15°方向有一艘澳方军舰C,求此时舰C与我舰航线AB的距离是多少?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCD中,点E在边DC上,DE=2,EC=1.把线段AE绕点A旋转,使点E落在直线BC上的点F处,连接DF,则tan∠CDF的值是
如图,正方形ABCD中,点E在边DC上,DE=2,EC=1.把线段AE绕点A旋转,使点E落在直线BC上的点F处,连接DF,则tan∠CDF的值是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
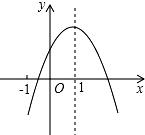 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com