
 如图,正方形ABCD中,点E在边DC上,DE=2,EC=1.把线段AE绕点A旋转,使点E落在直线BC上的点F处,连接DF,则tan∠CDF的值是
如图,正方形ABCD中,点E在边DC上,DE=2,EC=1.把线段AE绕点A旋转,使点E落在直线BC上的点F处,连接DF,则tan∠CDF的值是| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
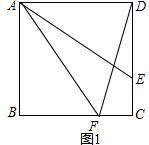 解:当F点在BC上,如图1,
解:当F点在BC上,如图1,
|
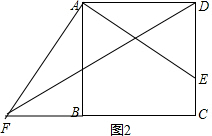
| CF |
| DC |
| 1 |
| 3 |
| CF |
| DC |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
 如图,边长为5km的正方形网格表示海平面示意图,其中阴影部分表示轮船无法通过的海域,甲轮船从A码头出发沿北偏东45°方向以10km/h的速度行驶20
如图,边长为5km的正方形网格表示海平面示意图,其中阴影部分表示轮船无法通过的海域,甲轮船从A码头出发沿北偏东45°方向以10km/h的速度行驶20| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=
如图,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=| m |
| x |
| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com